Semantics
From LLWiki
(Difference between revisions)
(Removed isomorphisms) |
(Reorganized page) |
||
| Line 1: | Line 1: | ||
| − | Linear Logic has numerous semantics some of which are described in details in the next sections. We give here an overview of the common properties that one may find in most of these models. We will denote by <math>A\longrightarrow B</math> the fact that there is a canonical morphism from <math>A</math> to <math>B</math> and by <math>A\cong B</math> the fact that there is a canonical isomorphism between <math>A</math> and <math>B</math>. By "canonical" we mean that these (iso)morphisms are natural transformations. |
+ | Linear Logic has numerous semantics some of which are described in details in the next sections. |
| + | * [[Coherent semantics]] |
||
| + | * [[Phase semantics]] |
||
| + | * [[Categorical semantics]] |
||
| + | * [[Relational semantics]] |
||
| + | * [[Finiteness semantics]] |
||
| + | * [[Geometry of interaction]] |
||
| + | * [[Game semantics]] |
||
| − | == Multiplicative semi-distributivity == |
+ | [[Provable formulas|Common properties]] may be found in most of these models. We will denote by <math>A\longrightarrow B</math> the fact that there is a canonical morphism from <math>A</math> to <math>B</math> and by <math>A\cong B</math> the fact that there is a canonical [[isomorphism]] between <math>A</math> and <math>B</math>. By "canonical" we mean that these (iso)morphisms are natural transformations. |
| − | |||
| − | <math> |
||
| − | \begin{array}{rcl} |
||
| − | A\tens(B\parr C) &\longrightarrow& (A\tens B)\parr C\\ |
||
| − | \end{array} |
||
| − | </math> |
||
| − | |||
| − | == Additive structure == |
||
| − | |||
| − | <math> |
||
| − | \begin{array}{rcl} |
||
| − | A\with B \longrightarrow A &\quad& A\with B \longrightarrow B\\ |
||
| − | (C\limp A)\with(C\limp B) &\longrightarrow& C\limp(A\with B)\\ |
||
| − | A &\longrightarrow& A\with A\\ |
||
| − | A \longrightarrow A\plus B &\quad& B \longrightarrow A\plus B\\ |
||
| − | (A\limp C)\with(B\limp C) &\longrightarrow& (A\plus B)\limp C\\ |
||
| − | A\plus A &\longrightarrow& A\\ |
||
| − | \end{array} |
||
| − | </math> |
||
| − | |||
| − | == Exponential structure == |
||
| − | |||
| − | <math> |
||
| − | \begin{array}{rclcrcl} |
||
| − | \oc A &\longrightarrow& A &\quad& A&\longrightarrow&\wn A\\ |
||
| − | \oc A &\longrightarrow& 1 &\quad& \bot &\longrightarrow& \wn A\\ |
||
| − | \oc A &\longrightarrow& \oc A\tens\oc A &\quad& |
||
| − | \wn A\parr\wn A &\longrightarrow& \wn A\\ |
||
| − | \oc A &\longrightarrow& \oc\oc A &\quad& \wn\wn A &\longrightarrow& \wn A\\ |
||
| − | \end{array} |
||
| − | </math> |
||
| − | |||
| − | == Monoidality of exponential == |
||
| − | |||
| − | <math> |
||
| − | \begin{array}{rclcrcl} |
||
| − | \oc A\tens\oc B &\longrightarrow& \oc(A\tens B) &\quad& |
||
| − | \one &\longrightarrow& \oc\one\\ |
||
| − | \end{array} |
||
| − | </math> |
||
Latest revision as of 20:58, 25 April 2013
Linear Logic has numerous semantics some of which are described in details in the next sections.
- Coherent semantics
- Phase semantics
- Categorical semantics
- Relational semantics
- Finiteness semantics
- Geometry of interaction
- Game semantics
Common properties may be found in most of these models. We will denote by 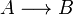 the fact that there is a canonical morphism from A to B and by
the fact that there is a canonical morphism from A to B and by 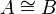 the fact that there is a canonical isomorphism between A and B. By "canonical" we mean that these (iso)morphisms are natural transformations.
the fact that there is a canonical isomorphism between A and B. By "canonical" we mean that these (iso)morphisms are natural transformations.