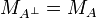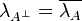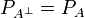Game semantics
This article presents the game-theoretic fully complete model of MLL. Formulas are interpreted by games between two players, Player and Opponent, and proofs are interpreted by strategies for Player.
Contents |
Preliminary definitions and notations
Sequences, Polarities
Definition (Sequences)
If M is a set of moves, a sequence or a play on M
is a finite sequence of elements of M. The set of sequences of M is denoted by M * .
We introduce some convenient notations on sequences.
- If
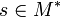 , | s | will denote the length of s;
, | s | will denote the length of s;
- If
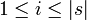 , si will denote the i-th move of s;
, si will denote the i-th move of s;
- We denote by
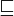 the prefix partial order on M * ;
the prefix partial order on M * ;
- If s1 is an even-length prefix of s2, we denote it by
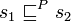 ;
;
- The empty sequence will be denoted by ε.
All moves will be equipped with a polarity, which will be either Player (P) or Opponent (O).
- We define
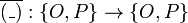 with
with 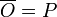 and
and 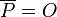 .
.
- This operation extends in a pointwise way to functions onto {O,P}.
Sequences on Components
We will often need to speak of sequences over (the disjoint sum of) multiple sets of moves, along with a restriction operation.
- If M1 and M2 are two sets, M1 + M2 will denote their disjoint sum, implemented as
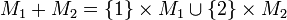 ;
;
- In this case, if we have two functions
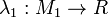 and
and 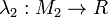 , we denote by
, we denote by ![[\lambda_1,\lambda_2]:M_1 + M_2 \to R](/mediawiki/images/math/d/d/2/dd25961a04d3f222a0c2ea007a70c4fb.png) their co-pairing;
their co-pairing;
- If
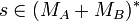 , the restriction of s to MA (resp. MB) is denoted by
, the restriction of s to MA (resp. MB) is denoted by 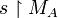 (resp.
(resp.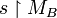 ). Later, if A and B are games, this will be abbreviated
). Later, if A and B are games, this will be abbreviated 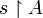 and
and 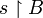 .
.
Games and Strategies
Game constructions
We first give the definition for a game, then all the constructions used to interpret the connectives and operations of MLL
Definition (Games)
A game A is a triple (MA,λA,PA) where:
- MA is a finite set of moves;
-
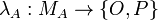 is a polarity function;
is a polarity function;
- PA is a subset of
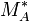 such that
such that
- Each
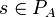 is alternating, i.e. if λA(si) = Q then, if defined,
is alternating, i.e. if λA(si) = Q then, if defined, 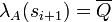 ;
;
- A is finite: there is no infinite strictly increasing sequence
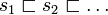 in PA.
in PA.
- Each
Definition (Linear Negation)
If A is a game, the game 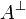 is A where Player and Opponent are interchanged. Formally:
is A where Player and Opponent are interchanged. Formally:
Definition (Tensor)
If A and B are games, we define 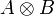 as:
as:
-
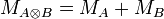 ;
;
-
![\lambda_{A\tens B} = [\lambda_A,\lambda_B]](/mediawiki/images/math/9/7/d/97d8367bc1429a3c5fb41bb0e4eb6f19.png)
-
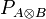 is the set of all finite, alternating sequences in
is the set of all finite, alternating sequences in 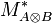 such that
such that 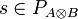 if and only if:
if and only if:
-
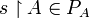 and
and 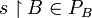 ;
;
- If we have
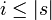 such that si and si + 1 are in different components, then
such that si and si + 1 are in different components, then 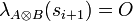 . We will refer to this condition as the switching convention for tensor game.
. We will refer to this condition as the switching convention for tensor game.
The par connective can be defined either as 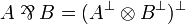 , or similarly to the tensor except that the switching convention is in favor of Player. We will refer to this as the switching convention for par game. Likewise, we define
, or similarly to the tensor except that the switching convention is in favor of Player. We will refer to this as the switching convention for par game. Likewise, we define 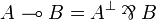 .
.
Strategies
Definition (Strategies)
A strategy for Player in a game A is defined as a subset 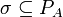 satisfying the following conditions:
satisfying the following conditions:
- σ is non-empty:
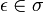
- Opponent starts: If
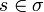 , λA(s1) = O;
, λA(s1) = O;
- σ is closed by even prefix, i.e. if
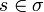 and
and 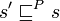 , then
, then 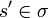 ;
;
- Determinacy: If we have
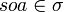 and
and 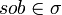 , then a = b.
, then a = b.
We write σ:A.
Composition is defined by parallel interaction plus hiding. We take all valid sequences on A,B and C which behave accordingly to σ (resp. τ) on A,B (resp. B,C). Then, we hide all the communication in B.
Definition (Parallel Interaction)
If A,B and C are games, we define the set of interactions
I(A,B,C) as the set of sequences s over A,B and C such that their respective restrictions on
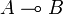 and
and 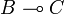 are in
are in 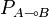 and
and 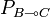 , and such that no successive
moves of s are respectively in A and C, or C and A.
If
, and such that no successive
moves of s are respectively in A and C, or C and A.
If 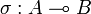 and
and 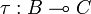 , we define the set of parallel interactions of
σ and τ, denoted by σ | | τ, as
, we define the set of parallel interactions of
σ and τ, denoted by σ | | τ, as 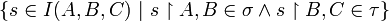 .
.
Definition (Composition)
If 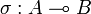 and
and 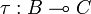 , we define
, we define 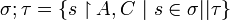 .
.
We also define the identities, which are simple copycat strategies : they immediately copy on the left (resp. right) component the last Opponent's move on the right (resp.left) component. In the following definition, let L (resp. R) denote the left (resp. right) occurrence of A in 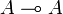 .
.
Definition (Identities)
If A is a game, we define a strategy 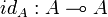 by
by 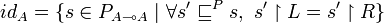 .
.
With these definitions, we get the following theorem:
Theorem (Category of Games and Strategies)
Composition of strategies is associative and identities are neutral for it. More precisely, there is a *-autonomous category with games as objects and strategies on 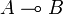 as morphisms from A to B.
as morphisms from A to B.