Categorical semantics
Constructing denotational models of linear can be a tedious work. Categorical semantics are useful to identify the fundamental structure of these models, and thus simplify and make more abstract the elaboration of those models.
TODO: why categories? how to extract categorical models? etc.
See [1]for a more detailed introduction to category theory. See [2]for a detailed treatment of categorical semantics of linear logic.
Contents |
Basic category theory recalled
Definition (Category)
Definition (Functor)
Definition (Natural transformation)
Definition (Adjunction)
Definition (Monad)
Overview
In order to interpret the various fragments of linear logic, we define incrementally what structure we need in a categorical setting.
- The most basic underlying structure are symmetric monoidal categories which model the symmetric tensor
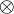 and its unit 1.
and its unit 1.
- The
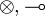 fragment (IMLL) is captured by so-called symmetric monoidal closed categories.
fragment (IMLL) is captured by so-called symmetric monoidal closed categories.
- Upgrading to ILL, that is, adding the exponential
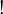 modality to IMLL requires modelling it categorically. There are various ways to do so: using rich enough adjunctions, or with an ad-hoc definition of a well-behaved comonad which leads to linear categories and close relatives.
modality to IMLL requires modelling it categorically. There are various ways to do so: using rich enough adjunctions, or with an ad-hoc definition of a well-behaved comonad which leads to linear categories and close relatives.
- Dealing with the additives
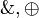 is quite easy, as they are plain cartesian product and coproduct, usually defined through universal properties in category theory.
is quite easy, as they are plain cartesian product and coproduct, usually defined through universal properties in category theory.
- Retrieving
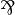 ,
, 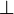 and
and 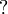 is just a matter of dualizing
is just a matter of dualizing 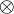 , 1 and
, 1 and 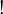 , thus requiring the model to be a *-autonomous category for that purpose.
, thus requiring the model to be a *-autonomous category for that purpose.
Modeling IMLL
A model of IMLL is a closed symmetric monoidal category. We recall the definition of these categories below.
Definition (Monoidal category)
A monoidal category 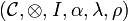 is a category
is a category 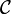 equipped with
equipped with
- a functor
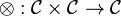 called tensor product,
called tensor product,
- an object I called unit object,
- three natural isomorphisms α, λ and ρ, called respectively associator, left unitor and right unitor, whose components are
such that
- for every objects A,B,C,D in
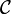 , the diagram
, the diagram
commutes,
- for every objects A and B in
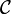 , the diagram
, the diagram
commutes.
Definition (Braided, symmetric monoidal category)
A braided monoidal category is a category together with a natural isomorphism of components
called braiding, such that the two diagrams
and
commute for every objects A, B and C.
A symmetric monoidal category is a braided monoidal category in which the braiding satisfies
for every objects A and B.
Definition (Closed monoidal category)
A monoidal category 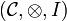 is left closed when for every object A, the functor
is left closed when for every object A, the functor
has a right adjoint, written
This means that there exists a bijection
which is natural in B and C. Equivalently, a monoidal category is left closed when it is equipped with a left closed structure, which consists of
- an object
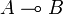 ,
,
- a morphism
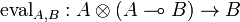 , called left evaluation,
, called left evaluation,
for every objects A and B, such that for every morphism 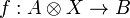 there exists a unique morphism
there exists a unique morphism 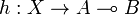 making the diagram
making the diagram
commute.
Dually, the monoidal category 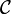 is right closed when the functor
is right closed when the functor 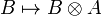 admits a right adjoint. The notion of right closed structure can be defined similarly.
admits a right adjoint. The notion of right closed structure can be defined similarly.
In a symmetric monoidal category, a left closed structure induces a right closed structure and conversely, allowing us to simply speak of a closed symmetric monoidal category.
Modeling the additives
Definition (Product)
A product (X,π1,π2) of two coinitial morphisms 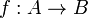 and
and 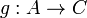 in a category
in a category 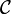 is an object X of
is an object X of 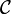 together with two morphisms
together with two morphisms 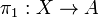 and
and 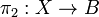 such that there exists a unique morphism
such that there exists a unique morphism 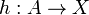 making the diagram
making the diagram
commute.
A category has finite products when it has products and a terminal object.
Definition (Monoid)
A monoid (M,μ,η) in a monoidal category 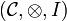 is an object M together with two morphisms
is an object M together with two morphisms
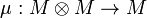 and
and 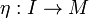
such that the diagrams
and
commute.
Property
Categories with products vs monoidal categories.
Modeling ILL
Introduced in[3].
Definition (Linear-non linear (LNL) adjunction)
A linear-non linear adjunction is a symmetric monoidal adjunction between lax monoidal functors
in which the category 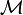 has finite products.
has finite products.
This section is devoted to defining the concepts necessary to define these adjunctions.
Definition (Monoidal functor)
A lax monoidal functor (F,f) between two monoidal categories 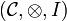 and
and 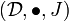 consists of
consists of
- a functor
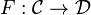 between the underlying categories,
between the underlying categories,
- a natural transformation f of components
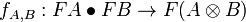 ,
,
- a morphism
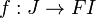
such that the diagrams
and
![\xymatrix{
FA\bullet J\ar[d]_{\rho_{FA}}\ar[r]^{FA\bullet\phi}&FA\bullet FI\ar[d]^{\phi_{A,I}}\\
FA&\ar[l]^{F\rho_A}F(A\otimes I)
}](/mediawiki/images/math/7/8/d/78d23ecd50d5cd94883b612058f77219.png) and
and ![\xymatrix{
J\bullet FB\ar[d]_{\lambda_{FB}}\ar[r]^{\phi\bullet FB}&FI\bullet FB\ar[d]^{\phi_{I,B}}\\
FB&\ar[l]^{F\lambda_B}F(I\otimes B)
}](/mediawiki/images/math/6/c/3/6c39c82c131aa6e4fdba1621c47dbea4.png)
commute for every objects A, B and C of 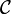 . The morphisms fA,B and f are called coherence maps.
. The morphisms fA,B and f are called coherence maps.
A lax monoidal functor is strong when the coherence maps are invertible and strict when they are identities.
Definition (Monoidal natural transformation)
Suppose that 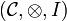 and
and 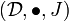 are two monoidal categories and
are two monoidal categories and
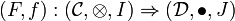 and
and 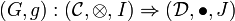
are two monoidal functors between these categories. A monoidal natural transformation 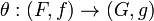 between these monoidal functors is a natural transformation
between these monoidal functors is a natural transformation 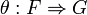 between the underlying functors such that the diagrams
between the underlying functors such that the diagrams
![\xymatrix{
FA\bullet FB\ar[d]_{f_{A,B}}\ar[r]^{\theta_A\bullet\theta_B}&\ar[d]^{g_{A,B}}GA\bullet GB\\
F(A\tens B)\ar[r]_{\theta_{A\tens B}}&G(A\tens B)
}](/mediawiki/images/math/3/2/f/32f1dfe7ceb90eee5904e637b7aec5dd.png) and
and ![\xymatrix{
&\ar[dl]_{f}J\ar[dr]^{g}&\\
FI\ar[rr]_{\theta_I}&&GI
}](/mediawiki/images/math/6/3/4/6341e967ecfa2c37d9a1b811cdfe4495.png)
commute for every objects A and B of 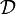 .
.
Definition (Monoidal adjunction)
A monoidal adjunction between two monoidal functors
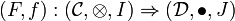 and
and 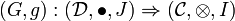
is an adjunction between the underlying functors F and G such that the unit and the counit
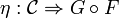 and
and 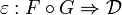
induce monoidal natural transformations between the corresponding monoidal functors.
Modeling negation
*-autonomous categories
Definition (*-autonomous category)
Suppose that we are given a symmetric monoidal closed category 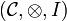 and an object R of
and an object R of 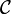 . For every object A, we define a morphism
. For every object A, we define a morphism
as follows. By applying the bijection of the adjunction defining (left) closed monoidal categories to the identity morphism 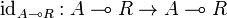 , we get a morphism
, we get a morphism 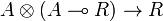 , and thus a morphism
, and thus a morphism 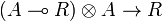 by precomposing with the symmetry
by precomposing with the symmetry 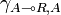 . The morphism
. The morphism 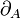 is finally obtained by applying the bijection of the adjunction defining (left) closed monoidal categories to this morphism. The object R is called dualizing when the morphism
is finally obtained by applying the bijection of the adjunction defining (left) closed monoidal categories to this morphism. The object R is called dualizing when the morphism 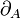 is a bijection for every object A of
is a bijection for every object A of 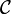 . A symmetric monoidal closed category is *-autonomous when it admits such a dualizing object.
. A symmetric monoidal closed category is *-autonomous when it admits such a dualizing object.
Compact closed categories
Definition (Dual objects)
A dual object structure 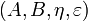 in a monoidal category
in a monoidal category 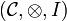 is a pair of objects A and B together with two morphisms
is a pair of objects A and B together with two morphisms
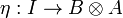 and
and 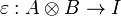
such that the diagrams
and
commute. The object A is called a left dual of B (and conversely B is a right dual of A).
Lemma
Two left (resp. right) duals of a same object B are necessarily isomorphic.
Definition (Compact closed category)
A symmetric monoidal category 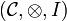 is compact closed when every object A has a right dual A * . We write
is compact closed when every object A has a right dual A * . We write
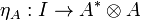 and
and 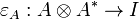
for the corresponding duality morphisms.
Lemma
In a compact closed category the left and right duals of an object A are isomorphic.
Property
A compact closed category 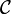 is monoidal closed, with closure defined by
is monoidal closed, with closure defined by
Proof.
To every morphism 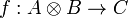 , we associate a morphism
, we associate a morphism 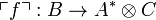 defined as
defined as
and to every morphism 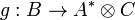 , we associate a morphism
, we associate a morphism 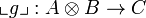 defined as
defined as
It is easy to show that 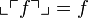 and
and 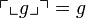 from which we deduce the required bijection.
from which we deduce the required bijection.
Property
A compact closed category is a (degenerated) *-autonomous category, with the obvious duality structure. In particular, 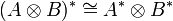 .
.
Remark: The above isomorphism does not hold in *-autonomous categories in general.
Proof. The dualizing object R is simply I * .
For any A, the reverse isomorphism 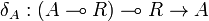 is constructed as follows:
is constructed as follows:
Identity on A is taken as the canonical morphism required.

![\xymatrix{
((A\otimes B)\otimes C)\otimes D\ar[d]_{\alpha_{A\otimes B,C,D}}\ar[r]^{\alpha_{A,B,C}\otimes D}&(A\otimes(B\otimes C))\otimes D\ar[r]^{\alpha_{A,B\otimes C,D}}&A\otimes((B\otimes C)\otimes D)\ar[d]^{A\otimes\alpha_{B,C,D}}\\
(A\otimes B)\otimes(C\otimes D)\ar[rr]_{\alpha_{A,B,C\otimes D}}&&A\otimes(B\otimes (C\otimes D))
}](/mediawiki/images/math/4/3/9/439465bf0734b4390e5cebc42a5467c7.png)
![\xymatrix{
(A\otimes I)\otimes B\ar[dr]_{\rho_A\otimes B}\ar[rr]^{\alpha_{A,I,B}}&&\ar[dl]^{A\otimes\lambda_B}A\otimes(I\otimes B)\\
&A\otimes B&
}](/mediawiki/images/math/8/8/c/88cb1e94216443b9db2d708253e8854c.png)
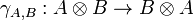
![\xymatrix{
&A\otimes(B\otimes C)\ar[r]^{\gamma_{A,B\otimes C}}&(B\otimes C)\otimes A\ar[dr]^{\alpha_{B,C,A}}\\
(A\otimes B)\otimes C\ar[ur]^{\alpha_{A,B,C}}\ar[dr]_{\gamma_{A,B}\otimes C}&&&B\otimes (C\otimes A)\\
&(B\otimes A)\otimes C\ar[r]_{\alpha_{B,A,C}}&B\otimes(A\otimes C)\ar[ur]_{B\otimes\gamma_{A,C}}\\
}](/mediawiki/images/math/f/a/0/fa07d4fc0a4aaed37b943dc152c823de.png)
![\xymatrix{
&(A\otimes B)\otimes C\ar[r]^{\gamma_{A\otimes B,C}}&C\otimes (A\otimes B)\ar[dr]^{\alpha^{-1}_{C,A,B}}&\\
A\otimes (B\otimes C)\ar[ur]^{\alpha^{-1}_{A,B,C}}\ar[dr]_{A\otimes\gamma_{B,C}}&&&(C\otimes A)\otimes B\\
&A\otimes(C\otimes B)\ar[r]_{\alpha^{-1}_{A,C,B}}&(A\otimes C)\otimes B\ar[ur]_{\gamma_{A,C}\otimes B}&\\
}](/mediawiki/images/math/f/2/c/f2c68065b9d14ab051200a8a1cf0a129.png)
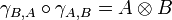
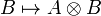
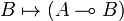
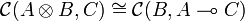
![\xymatrix{
A\tens X\ar@{.>}[d]_{A\tens h}\ar[dr]^{f}\\
A\tens(A\limp B)\ar[r]_-{\mathrm{eval}_{A,B}}&B
}](/mediawiki/images/math/f/4/6/f46f5ee5cdcdb18c234de0ae928e5f2f.png)
![\xymatrix{
&\ar[ddl]_fA\ar@{.>}[d]_h\ar[ddr]^g&\\
&\ar[dl]^{\pi_1}X\ar[dr]_{\pi_2}&\\
B&&C
}](/mediawiki/images/math/2/9/3/293f093e0781e1abb3edcb2f938678e1.png)
![\xymatrix{
&(M\tens M)\tens M\ar[dl]_{\alpha_{M,M,M}}\ar[r]^-{\mu\tens M}&M\tens M\ar[dd]^{\mu}\\
M\tens(M\tens M)\ar[d]_{M\tens\mu}&&\\
M\tens M\ar[rr]_{\mu}&&M\\
}](/mediawiki/images/math/4/c/0/4c0fd399ac7ac77daac182c99dcee184.png)
![\xymatrix{
I\tens M\ar[r]^{\eta\tens M}\ar[dr]_{\lambda_M}&M\tens M\ar[d]_\mu&\ar[l]_{M\tens\eta}\ar[dl]^{\rho_M}M\tens I\\
&M&
}](/mediawiki/images/math/9/2/4/924aa0337ed67af6e651d61dce494dc9.png)
![\xymatrix{
(\mathcal{M},\times,\top)\ar@/^/[rr]^{(L,l)}&\bot&\ar@/^/[ll]^{(M,m)}(\mathcal{L},\otimes,I)
}](/mediawiki/images/math/4/a/b/4abe488d46d4bb25aaac89ef54c834e1.png)
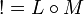
![\xymatrix{
(FA\bullet FB)\bullet FC\ar[d]_{\phi_{A,B}\bullet FC}\ar[r]^{\alpha_{FA,FB,FC}}&FA\bullet(FB\bullet FC)\ar[dr]^{FA\bullet\phi_{B,C}}\\
F(A\otimes B)\bullet FC\ar[dr]_{\phi_{A\otimes B,C}}&&FA\bullet F(B\otimes C)\ar[d]^{\phi_{A,B\otimes C}}\\
&F((A\otimes B)\otimes C)\ar[r]_{F\alpha_{A,B,C}}&F(A\otimes(B\otimes C))
}](/mediawiki/images/math/3/a/4/3a497fbd1997cd29d08ff588027586c9.png)
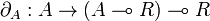
![\xymatrix{
&A\tens(B\tens A)\ar[r]^{\alpha_{A,B,A}^{-1}}&(A\tens B)\tens A\ar[dr]^{\varepsilon\tens A}\\
A\tens I\ar[ur]^{A\tens\eta}&&&I\tens A\ar[d]^{\lambda_A}\\
A\ar[u]^{\rho_A^{-1}}\ar@{=}[rrr]&&&A\\
}](/mediawiki/images/math/b/4/a/b4ad69c67d9740d8719ce74a1a8e7aea.png)
![\xymatrix{
&(B\tens A)\tens B\ar[r]^{\alpha_{B,A,B}}&B\tens(A\tens B)\ar[dr]^{B\tens\varepsilon}\\
I\tens B\ar[ur]^{\eta\tens B}&&&B\tens I\ar[d]^{\rho_B}\\
B\ar[u]^{\lambda_B^{-1}}\ar@{=}[rrr]&&&B\\
}](/mediawiki/images/math/6/c/0/6c00aa04cbdf618ed8ab78ac4fc72097.png)
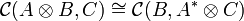
![\xymatrix{
B\ar[r]^-{\lambda_B^{-1}}&I\tens B\ar[r]^-{\eta_A\tens B}&(A^*\tens A)\tens B\ar[r]^-{\alpha_{A^*,A,B}}&A^*\tens(A\tens B)\ar[r]^-{A^*\tens f}&A\tens C\\
}](/mediawiki/images/math/a/c/2/ac2ef6bdfea1f929f7eedf069f5e5acc.png)
![\xymatrix{
A\tens B\ar[r]^-{A\tens g}&A\tens(A^*\tens C)\ar[r]^-{\alpha_{A,A^*,C}^{-1}}&(A\tens A^*)\tens C\ar[r]^-{\varepsilon_A\tens C}&I\tens C\ar[r]^-{\lambda_C}&C
}](/mediawiki/images/math/6/1/2/612d836a7aaf8dc88c2c04dca9dc94cd.png)