Isomorphism

This page is a stub and needs more content.

---

Two formulas A and B are isomorphic, when there are two proofs π of 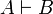$A \vdash B$ and ρ of 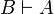$B \vdash A$ such that eliminating the cut on A in

$\AxRule{}\VdotsRule{\pi}{A \vdash B}\AxRule{}\VdotsRule{\rho}{B \vdash A}\LabelRule{\rulename{cut}}\BinRule{B\vdash B}\DisplayProof$

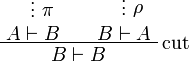
leads to an η-expansion of

$\LabelRule{\rulename{ax}}\NulRule{B\vdash B}\DisplayProof$,

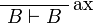and eliminating the cut on B in

$\AxRule{}\VdotsRule{\pi}{A \vdash B}\AxRule{}\VdotsRule{\rho}{B \vdash A}\LabelRule{\rulename{cut}}\BinRule{A\vdash A}\DisplayProof$

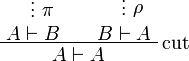
leads to an η-expansion of

$\LabelRule{\rulename{ax}}\NulRule{A\vdash A}\DisplayProof$.

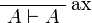Some well known isomorphisms of linear logic are the following ones:

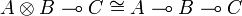
• $A\tens B \limp C \cong A\limp B \limp C$
• …