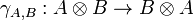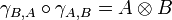Categorical semantics

TODO: why categories? how to extract categorical models? etc.

See for a more detailed introduction to category theory.

Modeling IMLL

A model of IMLL is a closed symmetric monoidal category. We recall the definition of these categories below.

Definition (Monoidal category)

A monoidal category 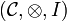$(\mathcal{C},\otimes,I)$ is a category 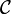$\mathcal{C}$ equipped with

• a functor 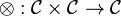$\otimes:\mathcal{C}\times\mathcal{C}\to\mathcal{C}$ called tensor product,
• an object I called unit object,
• three natural isomorphisms of components

$\alpha_{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C) \qquad \lambda_A:I\otimes A\to A \qquad \rho_A:A\otimes I\to A$

called respectively associator, left unitor and right unitor,

such that

• for every objects A,B,C,D in 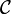$\mathcal{C}$, the diagram

commutes,

• for every objects A and B in 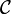$\mathcal{C}$, the diagrams

commute.

Definition (Braided, symmetric monoidal category)

A braided monoidal category is a category together with a natural isomorphism of components

$\gamma_{A,B}:A\otimes B\to B\otimes A$

called braiding, such that the two diagrams

UNIQ39775cce45daad23-math-0000000E-QINU

commute for every objects A, B and C.

A symmetric monoidal category is a braided monoidal category in which the braiding satisfies

$\gamma_{B,A}\circ\gamma_{A,B}=A\otimes B$

for every objects A and B.

Modeling negation

Definition (*-autonomous category)

TODO