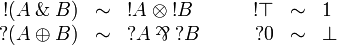Semantics

Linear Logic has numerous semantics some of which are described in details in the next sections. We give here an overview of the common properties that one may find in most of these models. We will denote by 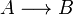$A\longrightarrow B$ the fact that there is a canonical morphism from A to B and by A˜B the fact that there is a canonical isomorphism between A and B. By "canonical" we mean that these (iso)morphisms are natural transformations.

Linear negation

$\begin{array}{rclcrcl} A\biorth &=& A\\ (A\tens B)\orth &\sim& A\orth\parr B\orth &\quad& \one\orth &\sim& \bot\\ (A\parr B)\orth &\sim& A\orth\tens B\orth &\quad& \bot\orth &\sim& \one\\ (A\with B)\orth &\sim& A\orth\plus B\orth &\quad& \top\orth &\sim& \zero\\ (A\plus B)\orth &\sim& A\orth\with B\orth &\quad& \zero\orth &\sim& \top\\ (\oc A)\orth &\sim& \wn A\orth\\ (\wn A)\orth &\sim& \oc A\orth\\[1ex] A\limp B &\sim& A\orth\parr B\\ A\limp B &\sim& B\orth\limp A\orth\\ \end{array}$

Neutrals

$\begin{array}{rcl} A\tens\one &\sim& \one\tens A\sim A\\ A\parr\bot &\sim& \bot\parr A\sim A\\ A\with\top &\sim& \top\with A\sim A\\ A\plus\zero &\sim&\zero\plus A\sim A\\ \end{array}$

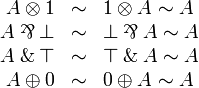
Commutativity

$\begin{array}{rcl} A\tens B &\sim& B\tens A\\ A\parr B &\sim& B\parr A\\ A\with B &\sim& B\with A\\ A\plus B &\sim& B\plus A\\ \end{array}$

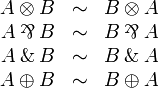
Associativity

$\begin{array}{rcl} (A\tens B)\tens C &\sim& A\tens(B\tens C)\\ (A\parr B)\parr C &\sim& A\parr(B\parr C)\\ (A\with B)\with C &\sim& A\with(B\with C)\\ (A\plus B)\plus C &\sim& A\plus(B\plus C)\\ \end{array}$

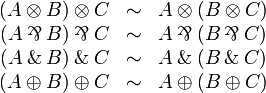
Multiplicative semi-distributivity

$\begin{array}{rcl} A\tens(B\parr C) &\longrightarrow& (A\tens B)\parr C\\ \end{array}$

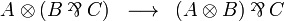
Multiplicative-additive distributivity

$\begin{array}{rclcrcl} A\tens(B\plus C) &\sim& (A\tens B)\plus(A\tens C) &\quad& A\tens\zero &\sim& \zero\\ A\parr(B\with C) &\sim& (A\parr B)\with(A\parr C) &\quad& A\parr\top &\sim& \top\\ \end{array}$

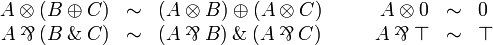
Additive structure

$\begin{array}{rcl} A\with B \longrightarrow A &\quad& A\with B \longrightarrow B\\ (C\limp A)\with(C\limp B) &\longrightarrow& C\limp(A\with B)\\ A \longrightarrow A\plus B &\quad& B \longrightarrow A\plus B\\ (A\limp C)\with(B\limp C) &\longrightarrow& (A\plus B)\limp C\\ \end{array}$

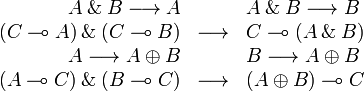
Exponential structure

$\begin{array}{rclcrcl} \oc A &\longrightarrow& A &\quad& A&\longrightarrow&\wn A\\ \oc A &\longrightarrow& 1 &\quad& \bot &\longrightarrow& \wn A\\ \oc A &\longrightarrow& \oc A\tens\oc A &\quad& \wn A\parr\wn A &\longrightarrow& \wn A\\ \oc A &\longrightarrow& \oc\oc A &\quad& \wn\wn A &\longrightarrow& \wn A\\ \end{array}$

Monoidality of exponential

$\begin{array}{rclcrcl} \oc A\tens\oc B &\longrightarrow& \oc(A\tens B) &\quad& \one &\longrightarrow& \oc\one\\ \end{array}$

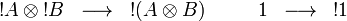
The exponential isomorphism

$\begin{array}{rclcrcl} \oc(A\with B) &\sim& \oc A\tens\oc B &\quad& \oc\top &\sim& \one\\ \wn(A\plus B) &\sim& \wn A\parr\wn B &\quad& \wn\zero &\sim& \bot\\ \end{array}$