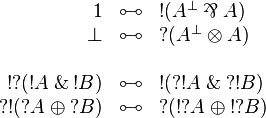List of equivalences

Each isomorphism gives an equivalence of formulas. The following equivalences are not isomorphisms.

Multiplicatives

$\begin{array}{rcccl} A &\linequiv& A \tens (A\orth\parr A) &\linequiv& (A\tens A\orth)\parr A \\ & & A\parr A\orth &\linequiv& (A\parr A\orth)\tens(A\parr A\orth) \end{array}$

Additives

$\begin{array}{rclcrcl} A \with A &\linequiv& A \\ A \plus A &\linequiv& A \\ \\ A \with (A \plus B) &\linequiv& A &\quad& A \plus \top &\linequiv& \top \\ A \plus (A \with B) &\linequiv& A &\quad& A \with \zero &\linequiv& \zero \end{array}$

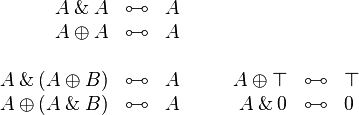
Quantifiers

$\begin{array}{rcll} \forall X.A &\linequiv& A &\quad (X\notin A) \\ \exists X.A &\linequiv& A &\quad (X\notin A) \end{array}$

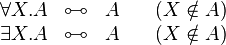
Exponentials

$\begin{array}{rclcrcl} \oc A &\linequiv& \oc A\tens\oc A &\quad& \wn A &\linequiv& \wn A\parr\wn A\\ \oc A &\linequiv& \oc\oc A &\quad& \wn A &\linequiv& \wn\wn A\\ \oc\wn A &\linequiv& \oc\wn\oc\wn A &\quad& \wn\oc A &\linequiv& \wn\oc\wn\oc A\\ \end{array}$

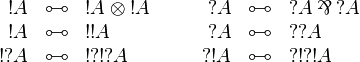
Some of these equivalences are related with the lattice of exponential modalities.

Polarities

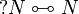
$\wn N \linequiv N$	(N negative)
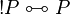
$\oc P \linequiv P$	(P positive)
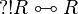
$\wn\oc R \linequiv R$	(R regular)
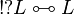
$\oc\wn L \linequiv L$	(L co-regular)

Second order encodings

$\begin{array}{rclcrcl} A &\linequiv &\forall X . (A \tens X\orth) \parr X \\ A &\linequiv &\exists X . (A \parr X\orth) \tens X \\ \\ A \with B &\linequiv& \exists X . \oc{(A \parr X\orth)} \tens \oc{(B \parr X\orth)} \tens X &\quad& \top &\linequiv& \exists X . X \\ A \plus B &\linequiv& \forall X . \wn{(A \tens X\orth)} \parr \wn{(B \tens X\orth)} \parr X &\quad& \zero &\linequiv& \forall X . X \\ \\ \bot &\linequiv& \exists X . X\tens X\orth \\ \one &\linequiv& \forall X . X\orth\parr X \\ \\ \forall \xi . A &\linequiv& \exists X . (\forall \xi . (A \parr X\orth)) \tens X \\ \exists \xi . A &\linequiv& \forall X . (\exists \xi . (A \tens X\orth)) \parr X \end{array}$

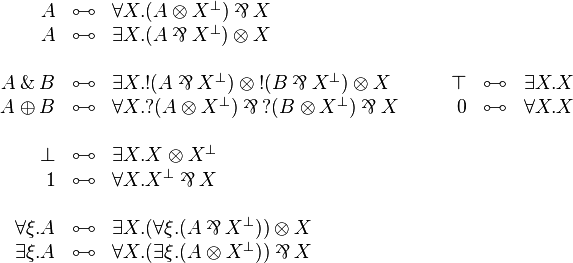
Miscellaneous

$\begin{array}{rcl} \one &\linequiv& \oc{(A\orth\parr A)} \\ \bot &\linequiv& \wn{(A\orth\tens A)} \\ \\ \oc{\wn{(\oc{A}\with\oc{B})}} &\linequiv& \oc{(\wn{\oc{A}}\with\wn{\oc{B}})} \\ \wn{\oc{(\wn{A}\plus\wn{B})}} &\linequiv& \wn{(\oc{\wn{A}}\plus\oc{\wn{B}})} \end{array}$