Coherent semantics
Coherent semantics was invented by Girard in the paper The system F, 15 years later. It is a refinement of the former qualitative domains that allows for building an interpretation of system F terms, that is for second order quantifiers.
Coherent semantics is based on the notion of stable functions that was initially proposed by Gérard Berry. Stability is a condition on Scott continuous functions that expresses the determinism of the relation between the output and the input: the typical Scott continuous but non stable function is the parallel or because when the two inputs are both set to true, only one of them is the reason why the result is true but there is no way to determine which one.
Although coherent semantics allowed to solve for the first time the old standing problem of building a denotationnal semantics for polymorphism, one of its main interest is that it also lead Girard to discover the notion of linear function, which rapidly gave rise to linear logic. It is one of the originality of linear logic that its syntax was derived from its semantics.
Contents |
Preliminary definitions and notations
There are two equivalent definitions of coherence spaces: the first one, coherent spaces as graphs, is the most commonly used and will be our "official" definition in the sequel. The second one, coherent spaces as domains, is however interesting from a historical point of view.
Coherent spaces
As graphs
Definition (Coherent space)
A coherent space X is a set of points denoted 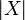 and called the web of X together with a reflexive and symetric relation
and called the web of X together with a reflexive and symetric relation 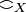 on
on 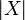 called the coherence relation. Coherent spaces are identified with the simple unoriented graphes of their coherence relations.
called the coherence relation. Coherent spaces are identified with the simple unoriented graphes of their coherence relations.
The strict coherence relation 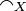 on X is defined by:
on X is defined by: 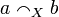 iff
iff 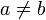 and
and 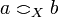 .
.
Definition (Clique)
A clique of the coherent space X is a set of points in 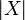 that are pairwise coherent. In other terms a clique is a subgraph of X that is complete. The set of cliques of X is denoted as
that are pairwise coherent. In other terms a clique is a subgraph of X that is complete. The set of cliques of X is denoted as 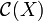 . We will often use the set of finite cliques of X that will be denoted
. We will often use the set of finite cliques of X that will be denoted 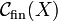 .
.
As domains
Definition (Coherent space)
A coherent space X is a family of subsets of a set 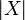 which is closed by subset (if
which is closed by subset (if 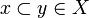 then
then 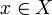 ) and satisfies the binary compatibility: if A is a family of pairwise compatible elements of X, that is if
) and satisfies the binary compatibility: if A is a family of pairwise compatible elements of X, that is if 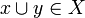 for any
for any 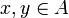 , then
, then 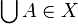 .
.
When viewed as a set ordered by inclusion a coherent space is particular case of domain. The reader will easily check that one recovers the previous definition by setting 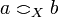 iff
iff 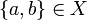 and conversely that the set of cliques of a coherent space in the graph sense is a coherent space in the domain sense. In particular finite cliques of X correspond to compact elements.
and conversely that the set of cliques of a coherent space in the graph sense is a coherent space in the domain sense. In particular finite cliques of X correspond to compact elements.
Stable functions
From now on we will identify the coherent space (in the graph sense) X with its set of cliques 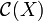 . Accordingly a function F from X to Y is a function defined on the cliques of X taking values in the cliques of Y.
. Accordingly a function F from X to Y is a function defined on the cliques of X taking values in the cliques of Y.
Definition (Stable function)
Let X and Y be two coherent spaces. A function 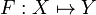 is stable if it satisfies:
is stable if it satisfies:
- it is non decreasing: for any
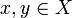 if
if 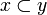 then
then 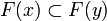 ;
;
- it is continuous (in the Scott sense): if A is a directed family of cliques of X, that is if for any
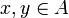 there is a
there is a 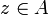 such that
such that 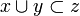 , then
, then 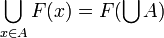 ;
;
- it satisfies the stability condition: if
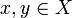 are compatible, that is if
are compatible, that is if 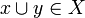 , then
, then 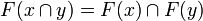 .
.
This definition is admitedly not very tractable. An equivalent and most useful caracterisation of stable functions is given by the following theorem.
Theorem
Let 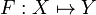 be a non-decreasing function from the coherent space X to the coherent space Y. The function F is stable iff it satisfies: for any
be a non-decreasing function from the coherent space X to the coherent space Y. The function F is stable iff it satisfies: for any 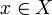 ,
, 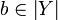 , if
, if 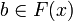 then there is a finite clique
then there is a finite clique 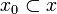 such that:
such that:
-
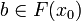 ,
,
- for any
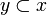 if
if 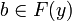 then
then 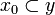 (x0 is the minimum sub-clique of x such that
(x0 is the minimum sub-clique of x such that 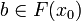 ).
).
Note that the stability condition doesn't depend on the coherent space structure and can be expressed more generally for continuous functions on domains. However the restriction to coherent spaces allows to get an interesting property: the set of stable functions from X to Y may be in turn endowed with a structure of coherent spaces. In categorical terms, the category of coherent spaces with stable functions is closed.
Definition (The space of stable functions)
Let X and Y be coherent spaces. The space 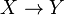 is defined by:
is defined by:
-
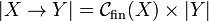 ,
,
-
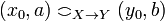 iff
iff 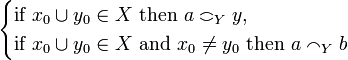 .
.
Theorem
Let X and Y be two coherent spaces. We denote by YX the set of stable functions from X to Y.