Intuitionistic linear logic
(Definition of ILL and embedding into LL (two-sided presentation)) |
(→The intuitionistic fragment of linear logic: refined statements) |
||
| Line 169: | Line 169: | ||
<math>JLL</math> is the [[fragment]] of linear logic obtained by restriction to intuitionistic formulas. |
<math>JLL</math> is the [[fragment]] of linear logic obtained by restriction to intuitionistic formulas. |
||
| − | {{Theorem|title=<math>JLL</math> and <math>ILL</math>| |
+ | {{Proposition|title=From <math>ILL</math> to <math>JLL</math>| |
| − | <math>\Gamma\vdash A</math> is provable in <math>ILL_1</math> if and only if it is provable in <math>JLL_1</math>. |
+ | If <math>\Gamma\vdash A</math> is provable in <math>ILL_{012}</math>, it is provable in <math>JLL_{012}</math>. |
}} |
}} |
||
{{Proof| |
{{Proof| |
||
| − | The first direction is immediate since <math>ILL_1</math> is included in <math>JLL_1</math>. |
+ | <math>ILL_{012}</math> is included in <math>JLL_{012}</math>. |
| + | }} |
||
| − | For the second direction, we consider a cut-free proof of <math>\Gamma\vdash A</math> in <math>JLL_1</math>. We prove by induction on the length of such a proof that it belongs to <math>ILL_1</math>. |
+ | {{Theorem|title=From <math>JLL</math> to <math>ILL</math>| |
| + | If <math>\Gamma\vdash\Delta</math> is provable in <math>JLL_{12}</math>, it is provable in <math>ILL_{12}</math>. |
||
}} |
}} |
||
| + | {{Proof| |
||
| + | We only prove the first order case, a proof of the full result is given in the PhD thesis of Harold Schellinx<ref>{{BibEntry|bibtype=phdthesis|author=Schellinx, Harold|title=The Noble Art of Linear Decorating|type=Dissertation series of the Dutch Institute for Logic, Language and Computation|school=University of Amsterdam|note=ILLC-Dissertation Series, 1994-1|year=1994}}</ref>. |
||
| + | |||
| + | Consider a cut-free proof of <math>\Gamma\vdash\Delta</math> in <math>JLL_{12}</math>, we can prove by induction on the length of such a proof that it belongs to <math>ILL_{12}</math>. |
||
| + | }} |
||
| + | |||
| + | {{Corollary|title=Unique conclusion in <math>JLL</math>| |
||
| + | If <math>\Gamma\vdash\Delta</math> is provable in <math>JLL_{12}</math> then <math>\Delta</math> is a singleton. |
||
| + | }} |
||
| − | This result is still valid with units from <math>ILL_1</math> into <math>JLL_1</math>. In the opposite direction, it holds with <math>\one</math> but not anymore with <math>\top</math> and <math>\zero</math>. <math>{}\vdash((X\limp Y)\limp\zero)\limp(X\tens\top)</math> is provable in <math>JLL_1</math>: |
+ | The theorem is still valid with for formulas containing <math>\one</math> but not anymore with <math>\top</math> and <math>\zero</math>. <math>{}\vdash((X\limp Y)\limp\zero)\limp(X\tens\top)</math> is provable in <math>JLL_0</math>: |
<math> |
<math> |
||
| Line 200: | Line 209: | ||
</math> |
</math> |
||
| − | but not in <math>ILL_1</math>. |
+ | but not in <math>ILL_0</math>. |
| + | |||
| + | == References == |
||
| + | <references /> |
||
Revision as of 20:46, 11 January 2009
Intuitionistic Linear Logic (ILL) is the
intuitionnistic restriction of linear logic: the sequent calculus
of ILL is obtained from the two-sided sequent calculus of
linear logic by constraining sequents to have exactly one formula on
the right-hand side: 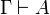 .
.
The connectives 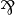 ,
, 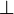 and
and 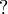 are
not available anymore, but the linear implication
are
not available anymore, but the linear implication 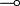 is.
is.
Sequent Calculus
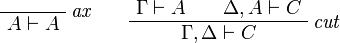
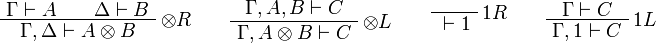
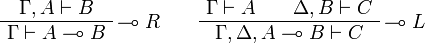
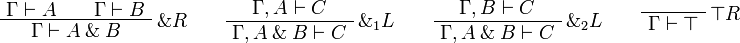
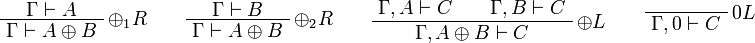
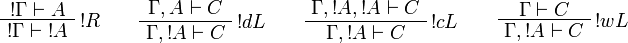
![\AxRule{\Gamma\vdash A}
\LabelRule{\forall R}
\UnaRule{\Gamma\vdash \forall\alpha A}
\DisplayProof
\qquad
\AxRule{\Gamma,A[\tau/\alpha]\vdash C}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\alpha A\vdash C}
\DisplayProof
\qquad
\AxRule{\Gamma\vdash A[\tau/\alpha]}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash\exists\alpha A}
\DisplayProof
\qquad
\AxRule{\Gamma,A\vdash C}
\LabelRule{\exists L}
\UnaRule{\Gamma,\exists\alpha A\vdash C}
\DisplayProof](/mediawiki/images/math/a/9/5/a95dbb5013cc708c2470ee8327494607.png)
with α not free in Γ,C in the rules 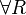 and
and 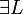 .
.
The intuitionistic fragment of linear logic
In order to characterize intuitionistic linear logic inside linear logic, we define the intuitionistic restriction of linear formulas:
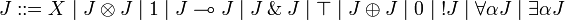
JLL is the fragment of linear logic obtained by restriction to intuitionistic formulas.
Proposition (From ILL to JLL)
If 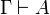 is provable in ILL012, it is provable in JLL012.
is provable in ILL012, it is provable in JLL012.
Proof. ILL012 is included in JLL012.
Theorem (From JLL to ILL)
If 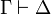 is provable in JLL12, it is provable in ILL12.
is provable in JLL12, it is provable in ILL12.
Proof. We only prove the first order case, a proof of the full result is given in the PhD thesis of Harold Schellinx[1].
Consider a cut-free proof of 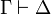 in JLL12, we can prove by induction on the length of such a proof that it belongs to ILL12.
in JLL12, we can prove by induction on the length of such a proof that it belongs to ILL12.
Corollary (Unique conclusion in JLL)
If 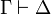 is provable in JLL12 then Δ is a singleton.
is provable in JLL12 then Δ is a singleton.
The theorem is still valid with for formulas containing 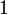 but not anymore with
but not anymore with 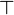 and
and 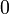 .
. 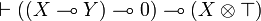 is provable in JLL0:
is provable in JLL0:
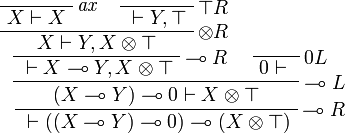
but not in ILL0.
References
- ↑ Schellinx, Harold. The Noble Art of Linear Decorating. Dissertation series of the Dutch Institute for Logic, Language and Computation. University of Amsterdam. ILLC-Dissertation Series, 1994-1, 1994.