Notations
From LLWiki
(Difference between revisions)
(first set of notations) |
(→Formulas: substitutions) |
||
| Line 50: | Line 50: | ||
=== Formulas === |
=== Formulas === |
||
| − | * First order quantification: <math>\forall x A</math> |
+ | * First order quantification: <math>\forall x A</math> with substitution <math>A[t/x]</math> |
| − | * Second order quantification: <math>\forall X A</math> |
+ | * Second order quantification: <math>\forall X A</math> with substitution <math>A[B/X]</math> |
| − | * Quantification of arbitrary order (mainly first or second): <math>\forall\alpha A</math> |
+ | * Quantification of arbitrary order (mainly first or second): <math>\forall\alpha A</math> with substitution <math>A[\tau/\alpha]</math> |
=== Rule names === |
=== Rule names === |
||
Revision as of 19:51, 7 January 2009
Contents |
Logical systems
For a given logical system such as MLL (for multiplicative linear logic), we consider the following variations:
| Notation | Meaning | Connectives |
|---|---|---|
| MLL | propositional without units | 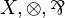
|
| MLLu | propositional with units only | 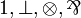
|
| MLL0 | propositional with units and variables | 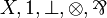
|
| MLL1 | first-order without units | 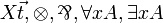
|
| MLL01 | first-order with units | 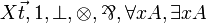
|
| MLL2 | second-order propositional without units | 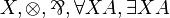
|
| MLL02 | second-order propositional with units | 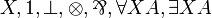
|
| MLL12 | first-order and second-order without units | 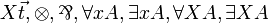
|
| MLL012 | first-order and second-order with units | 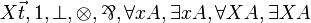
|
Formulas and proof trees
Formulas
- First order quantification:
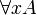 with substitution A[t / x]
with substitution A[t / x]
- Second order quantification:
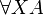 with substitution A[B / X]
with substitution A[B / X]
- Quantification of arbitrary order (mainly first or second):
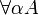 with substitution A[τ / α]
with substitution A[τ / α]
Rule names
Name of the connective, followed by some additional information if required, followed by "L" for a left rule or "R" for a right rule.
For example: 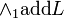 .
.