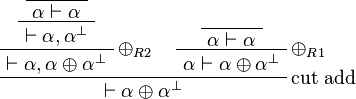Additive cut rule

From LLWiki
(Difference between revisions)
Jump to: navigation, search
(Non admissibility)
 

Latest revision as of 21:24, 28 October 2013

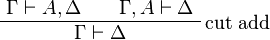
The additive cut rule is: \AxRule{\Gamma\vdash A,\Delta} \AxRule{\Gamma,A\vdash\Delta} \LabelRule{\rulename{cut\;add}} \BinRule{\Gamma\vdash\Delta} \DisplayProof

In contrary to what happens in classical logic, this rule is not admissible in linear logic.

The formula 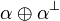\alpha\plus\alpha\orth is not provable in linear logic, while it is derivable with the additive cut rule:

\NulRule{\alpha\vdash\alpha} \UnaRule{\vdash\alpha,\alpha\orth} \LabelRule{\plus_{R2}} \UnaRule{\vdash\alpha,\alpha\plus\alpha\orth} \NulRule{\alpha\vdash\alpha} \LabelRule{\plus_{R1}} \UnaRule{\alpha\vdash\alpha\plus\alpha\orth} \LabelRule{\rulename{cut\;add}} \BinRule{\vdash\alpha\plus\alpha\orth} \DisplayProof

Retrieved from "http://140.77.166.78/mediawiki/index.php?title=Additive_cut_rule&oldid=612"
Personal tools