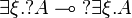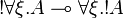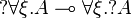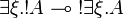Provable formulas

From LLWiki
(Difference between revisions)
Jump to: navigation, search
m (Modified order of sections)
(→‎Factorizations: exists/plus added)
Line 28: Line 28:
   
 
<math>(A\parr B)\plus (A\parr C) \limp A\parr (B\plus C)</math>
  
<math>(A\parr B)\plus (A\parr C) \limp A\parr (B\plus C)</math>
  +
  +
<math>(\forall \xi . A) \plus (\forall \xi . B) \limp \forall \xi . (A \plus B)</math>
   
 
== Additive structure ==
  
== Additive structure ==

Revision as of 20:30, 28 October 2013

This page is a stub and needs more content.

Important provable formulas are given by isomorphisms and by equivalences.

In many of the cases below the converse implication does not hold.

Contents

Distributivities

Standard distributivities

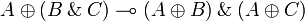
A\plus (B\with C) \limp (A\plus B)\with (A\plus C)

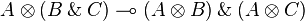
A\tens (B\with C) \limp (A\tens B)\with (A\tens C)

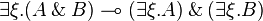
\exists \xi . (A \with B) \limp (\exists \xi . A) \with (\exists \xi . B)

Linear distributivities

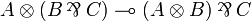
A\tens (B\parr C) \limp (A\tens B)\parr C

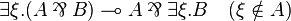
\exists \xi. (A \parr B) \limp A \parr \exists \xi.B \quad (\xi\notin A)

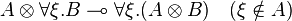
A \tens \forall \xi.B \limp \forall \xi. (A \tens B) \quad (\xi\notin A)

Factorizations

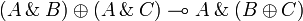
(A\with B)\plus (A\with C) \limp A\with (B\plus C)

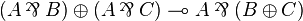
(A\parr B)\plus (A\parr C) \limp A\parr (B\plus C)

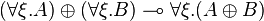
(\forall \xi . A) \plus (\forall \xi . B) \limp \forall \xi . (A \plus B)

Additive structure

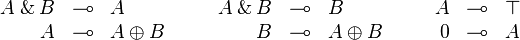
\begin{array}{rclcrclcrcl} A\with B &\limp& A &\quad& A\with B &\limp& B &\quad& A &\limp& \top\\ A &\limp& A\plus B &\quad& B &\limp& A\plus B &\quad& \zero &\limp& A \end{array}

Quantifiers

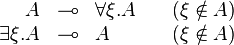
\begin{array}{rcll} A &\limp& \forall \xi.A &\quad (\xi\notin A) \\ \exists \xi.A &\limp& A &\quad (\xi\notin A) \end{array}


\begin{array}{rcl} \forall \xi_1.\forall \xi_2. A &\limp& \forall \xi. A[^\xi/_{\xi_1},^\xi/_{\xi_2}] \\ \exists \xi.A[^\xi/_{\xi_1},^\xi/_{\xi_2}] &\limp& \exists \xi_1. \exists \xi_2.A \end{array}

Exponential structure

Provable formulas involving exponential connectives only provide us with the lattice of exponential modalities.

\begin{array}{rclcrcl} \oc A &\limp& A &\quad& A&\limp&\wn A\\ \oc A &\limp& 1 &\quad& \bot &\limp& \wn A \end{array}

Monoidality of exponentials

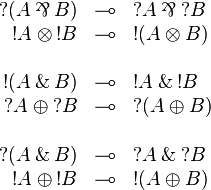
\begin{array}{rcl} \wn(A\parr B) &\limp& \wn A\parr\wn B \\ \oc A\tens\oc B &\limp& \oc(A\tens B) \\ \\ \oc{(A \with B)} &\limp& \oc{A} \with \oc{B} \\ \wn{A} \plus \wn{B} &\limp& \wn{(A \plus B)} \\ \\ \wn{(A \with B)} &\limp& \wn{A} \with \wn{B} \\ \oc{A} \plus \oc{B} &\limp& \oc{(A \plus B)} \end{array}

Promotion principles

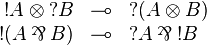
\begin{array}{rcl} \oc{A} \tens \wn{B} &\limp& \wn{(A \tens B)} \\ \oc{(A \parr B)} &\limp& \wn{A} \parr \oc{B} \end{array}

Commutations

\exists \xi . \wn A \limp \wn{\exists \xi . A}

\oc{\forall \xi . A} \limp \forall \xi . \oc A

\wn{\forall \xi . A} \limp \forall \xi . \wn A

\exists \xi . \oc A \limp \oc{\exists \xi . A}

Retrieved from "http://140.77.166.78/mediawiki/index.php?title=Provable_formulas&oldid=610"
Personal tools