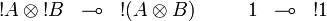Provable formulas
From LLWiki
(Difference between revisions)
(Added formules from Semantics page) |
m (\limp instead of \longrightarrow) |
||
| Line 17: | Line 17: | ||
<math> |
<math> |
||
\begin{array}{rcl} |
\begin{array}{rcl} |
||
| − | A\with B \longrightarrow A &\quad& A\with B \longrightarrow B\\ |
+ | A\with B \limp A &\quad& A\with B \limp B\\ |
| − | (C\limp A)\with(C\limp B) &\longrightarrow& C\limp(A\with B)\\ |
+ | (C\limp A)\with(C\limp B) &\limp& C\limp(A\with B)\\ |
| − | A &\longrightarrow& A\with A\\ |
+ | A &\limp& A\with A\\ |
| − | A \longrightarrow A\plus B &\quad& B \longrightarrow A\plus B\\ |
+ | A \limp A\plus B &\quad& B \limp A\plus B\\ |
| − | (A\limp C)\with(B\limp C) &\longrightarrow& (A\plus B)\limp C\\ |
+ | (A\limp C)\with(B\limp C) &\limp& (A\plus B)\limp C\\ |
| − | A\plus A &\longrightarrow& A\\ |
+ | A\plus A &\limp& A\\ |
\end{array} |
\end{array} |
||
</math> |
</math> |
||
| Line 32: | Line 32: | ||
<math> |
<math> |
||
\begin{array}{rclcrcl} |
\begin{array}{rclcrcl} |
||
| − | \oc A &\longrightarrow& A &\quad& A&\longrightarrow&\wn A\\ |
+ | \oc A &\limp& A &\quad& A&\limp&\wn A\\ |
| − | \oc A &\longrightarrow& 1 &\quad& \bot &\longrightarrow& \wn A\\ |
+ | \oc A &\limp& 1 &\quad& \bot &\limp& \wn A\\ |
| − | \oc A &\longrightarrow& \oc A\tens\oc A &\quad& |
+ | \oc A &\limp& \oc A\tens\oc A &\quad& |
| − | \wn A\parr\wn A &\longrightarrow& \wn A\\ |
+ | \wn A\parr\wn A &\limp& \wn A\\ |
| − | \oc A &\longrightarrow& \oc\oc A &\quad& \wn\wn A &\longrightarrow& \wn A\\ |
+ | \oc A &\limp& \oc\oc A &\quad& \wn\wn A &\limp& \wn A\\ |
\end{array} |
\end{array} |
||
</math> |
</math> |
||
| Line 44: | Line 44: | ||
<math> |
<math> |
||
\begin{array}{rclcrcl} |
\begin{array}{rclcrcl} |
||
| − | \oc A\tens\oc B &\longrightarrow& \oc(A\tens B) &\quad& |
+ | \oc A\tens\oc B &\limp& \oc(A\tens B) &\quad& |
| − | \one &\longrightarrow& \oc\one\\ |
+ | \one &\limp& \oc\one\\ |
\end{array} |
\end{array} |
||
</math> |
</math> |
||
Revision as of 21:05, 25 April 2013
This page is a stub and needs more content.
In many of the cases below the converse implication does not hold.
Contents |
Distributivities
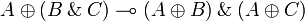
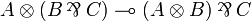
Factorizations
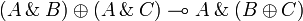
Additive structure
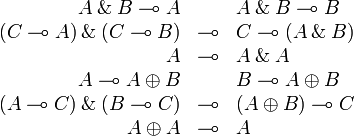
Exponential structure
Provable formulas involving exponential connectives only provide us with the lattice of exponential modalities.
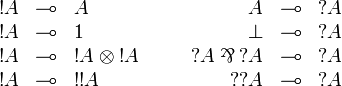
Monoidality of exponential