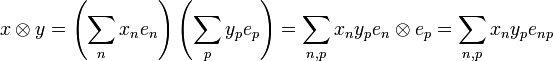GoI for MELL: exponentials
From LLWiki
(Difference between revisions)
(Creation of the page : generalities on Hilbert spaces tensor product) |
Revision as of 09:28, 25 May 2010
The tensor product of Hilbert spaces</math>
Recall that 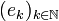 is the canonical basis of
is the canonical basis of 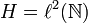 . The space
. The space 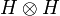 is the collection of sequences
is the collection of sequences 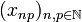 of complex numbers such that:
of complex numbers such that:
| ∑ | | xnp | 2 |
| n,p |
converges. The scalar product is defined just as before:
-
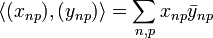 .
.
The canonical basis of 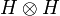 is denoted
is denoted 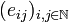 where eij is the (doubly indexed) sequence
where eij is the (doubly indexed) sequence 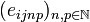 defined by:
defined by:
- eijnp = δinδjp (all terms are null but the one at index (i,j) which is 1).
If 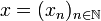 and
and 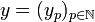 are vectors in H then their tensor is the sequence:
are vectors in H then their tensor is the sequence:
-
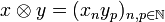 .
.
In particular we have: 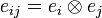 and we can write:
and we can write: