Notations
From LLWiki
(Difference between revisions)
Lionel Vaux (Talk | contribs) (→Semantics: Notations for finiteness spaces) |
Lionel Vaux (Talk | contribs) m (→Finiteness spaces: justify the notation of fniiteness structures) |
||
| Line 66: | Line 66: | ||
=== [[Finiteness spaces]] === |
=== [[Finiteness spaces]] === |
||
| − | * Web of the space <math>\mathcal A</math>: <math>\web {\mathcal A}</math> |
+ | * Web of the finiteness space <math>\mathcal A</math>: <math>\web{\mathcal A}</math> |
| − | * Finiteness structure of the space <math>\mathcal A</math>: <math>\mathfrak F(\mathcal A)</math> |
+ | * Finiteness structure of the space <math>\mathcal A</math>: <math>\mathfrak F(\mathcal A)</math> (we use <tt>\mathfrak</tt>, which is consistent with the fact that <math>\finpowerset{\web{\mathcal A}}\subseteq \mathfrak F(\mathcal A) \subseteq\powerset{\web{\mathcal A}}</math>). |
Revision as of 15:48, 6 July 2009
Contents |
Logical systems
For a given logical system such as MLL (for multiplicative linear logic), we consider the following variations:
| Notation | Meaning | Connectives |
|---|---|---|
| MLL | propositional without units |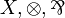 
|
| MLLu | propositional with units only |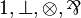 
|
| MLL0 | propositional with units and variables |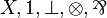 
|
| MLL1 | first-order without units |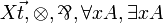 
|
| MLL01 | first-order with units |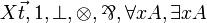 
|
| MLL2 | second-order propositional without units |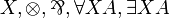 
|
| MLL02 | second-order propositional with units |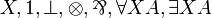 
|
| MLL12 | first-order and second-order without units |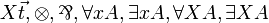 
|
| MLL012 | first-order and second-order with units |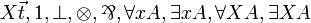 
|
Formulas and proof trees
Formulas
- First order quantification:
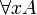with substitution A[t / x]
- Second order quantification:
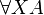with substitution A[B / X]
- Quantification of arbitrary order (mainly first or second):
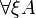with substitution A[τ / ξ]
Rule names
Name of the connective, followed by some additional information if required, followed by "L" for a left rule or "R" for a right rule. This is for a two-sided system, "R" is implicit for one-sided systems.
For example: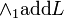 
.
Semantics
Coherent spaces
- Web of the space X:
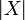
- Coherence relation of the space X: large
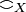and strict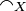 
Finiteness spaces
- Web of the finiteness space
: 
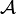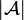
- Finiteness structure of the space :
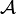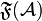(we use \mathfrak, which is consistent with the fact that 
).
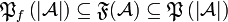