Relational semantics
From LLWiki
(Difference between revisions)
(New page: == Relational semantics == This is the simplest denotational semantics of linear logic. It consists in interpreting a formula <math>A</math> as a set <math>A^*</math> and a proof <math>\p...) |
Revision as of 21:47, 14 March 2009
Relational semantics
This is the simplest denotational semantics of linear logic. It consists in interpreting a formula A as a set A * and a proof π of A as a subset π * of A * .
The category of sets and relations
It is the category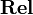 
whose objects are sets, and such that 
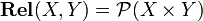. Composition is the ordinary composition of relations: given 
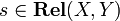and 
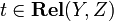, one
sets
.
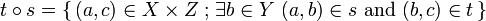