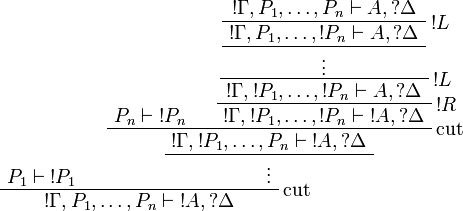Positive formula

Revision as of 16:53, 12 March 2009

A positive formula is a formula $P$ such that 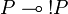$P\limp\oc P$ (thus a coalgebra for the comonad 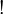$\oc$ ). As a consequence $P$ and 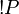$\oc P$ are equivalent.

Positive connectives

A connective $c$ of arity $n$ is positive if for any positive formulas $P 1$ ,..., $P n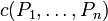$ , $c(P_1,\dots,P_n)$ is positive.

Proposition (Positive connectives)

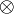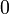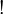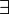$\tens$ , $\one$ , $\plus$ , $\zero$ , $\oc$ and $\exists$ are positive connectives.

Proof. $\AxRule{P_2\vdash\oc{P_2}} \AxRule{P_1\vdash\oc{P_1}} \LabelRule{\rulename{ax}} \NulRule{P_1\vdash P_1} \LabelRule{\rulename{ax}} \NulRule{P_2\vdash P_2} \LabelRule{\tens R} \BinRule{P_1,P_2\vdash P_1\tens P_2} \LabelRule{\oc d L} \UnaRule{\oc{P_1},P_2\vdash P_1\tens P_2} \LabelRule{\oc d L} \UnaRule{\oc{P_1},\oc{P_2}\vdash P_1\tens P_2} \LabelRule{\oc R} \UnaRule{\oc{P_1},\oc{P_2}\vdash\oc{(P_1\tens P_2)}} \LabelRule{\rulename{cut}} \BinRule{P_1,\oc{P_2}\vdash\oc{(P_1\tens P_2)}} \LabelRule{\rulename{cut}} \BinRule{P_1,P_2\vdash\oc{(P_1\tens P_2)}} \LabelRule{\tens L} \UnaRule{P_1\tens P_2\vdash\oc{(P_1\tens P_2)}} \DisplayProof$

$\LabelRule{\one R} \NulRule{\vdash\one} \LabelRule{\oc R} \UnaRule{\vdash\oc{\one}} \LabelRule{\one L} \UnaRule{\one\vdash\oc{\one}} \DisplayProof$

$\AxRule{P_1\vdash\oc{P_1}} \LabelRule{\rulename{ax}} \NulRule{P_1\vdash P_1} \LabelRule{\plus_1 R} \UnaRule{P_1\vdash P_1\plus P_2} \LabelRule{\oc d L} \UnaRule{\oc{P_1}\vdash P_1\plus P_2} \LabelRule{\oc R} \UnaRule{\oc{P_1}\vdash\oc{(P_1\plus P_2)}} \LabelRule{\rulename{cut}} \BinRule{P_1\vdash\oc{(P_1\plus P_2)}} \AxRule{P_2\vdash\oc{P_2}} \LabelRule{\rulename{ax}} \NulRule{P_2\vdash P_2} \LabelRule{\plus_2 R} \UnaRule{P_2\vdash P_1\plus P_2} \LabelRule{\oc d L} \UnaRule{\oc{P_2}\vdash P_1\plus P_2} \LabelRule{\oc R} \UnaRule{\oc{P_2}\vdash\oc{(P_1\plus P_2)}} \LabelRule{\rulename{cut}} \BinRule{P_2\vdash\oc{(P_1\plus P_2)}} \LabelRule{\plus L} \BinRule{P_1\plus P_2\vdash\oc{(P_1\plus P_2)}} \DisplayProof$

$\LabelRule{\zero L} \NulRule{\zero\vdash\oc{\zero}} \DisplayProof$

$\LabelRule{\rulename{ax}} \NulRule{\oc{P}\vdash\oc{P}} \LabelRule{\oc R} \UnaRule{\oc{P}\vdash\oc{\oc{P}}} \DisplayProof$

$\AxRule{P\vdash\oc{P}} \LabelRule{\rulename{ax}} \NulRule{P\vdash P} \LabelRule{\exists R} \UnaRule{P\vdash \exists\xi P} \LabelRule{\oc d L} \UnaRule{\oc{P}\vdash \exists\xi P} \LabelRule{\oc R} \UnaRule{\oc{P}\vdash\oc{\exists\xi P}} \LabelRule{\rulename{cut}} \BinRule{P\vdash\oc{\exists\xi P}} \LabelRule{\exists L} \UnaRule{\exists\xi P\vdash\oc{\exists\xi P}} \DisplayProof$

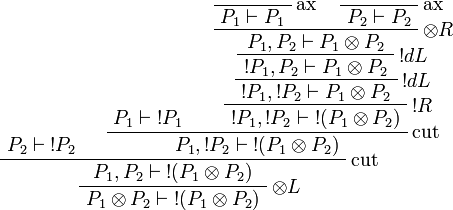
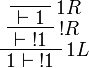
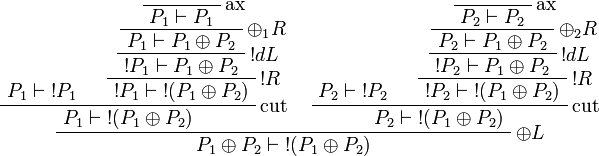
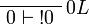
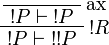
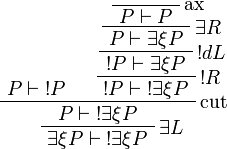
More generally, 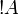$\oc A$ is positive for any formula $A$ .

The notion of positive connective is related with but different from the notion of asynchronous connective.

Generalized structural rules

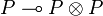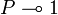Positive formulas admit generalized left structural rules corresponding to a structure of $\tens$ -comonoid: $P\limp P\tens P$ and $P\limp\one$ . The following rule is derivable:

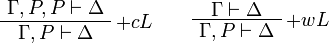
$\AxRule{\Gamma,P,P\vdash\Delta} \LabelRule{+ c L} \UnaRule{\Gamma,P\vdash\Delta} \DisplayProof \qquad \AxRule{\Gamma\vdash\Delta} \LabelRule{+ w L} \UnaRule{\Gamma,P\vdash\Delta} \DisplayProof$

Proof. $\AxRule{P\vdash\oc{P}} \AxRule{\Gamma,P,P\vdash\Delta} \LabelRule{\oc L} \UnaRule{\Gamma,P,\oc P\vdash\Delta} \LabelRule{\oc L} \UnaRule{\Gamma,\oc P,\oc P\vdash\Delta} \LabelRule{\oc c L} \UnaRule{\Gamma,\oc P\vdash\Delta} \LabelRule{\rulename{cut}} \BinRule{\Gamma,P\vdash\Delta} \DisplayProof$

$\AxRule{P\vdash\oc{P}} \AxRule{\Gamma\vdash\Delta} \LabelRule{\oc w L} \UnaRule{\Gamma,\oc P\vdash\Delta} \LabelRule{\rulename{cut}} \BinRule{\Gamma,P\vdash\Delta} \DisplayProof$

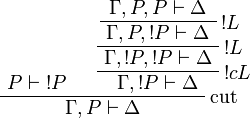
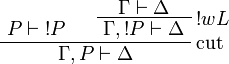
Positive formulas are also acceptable in the left-hand side context of the promotion rule. The following rule is derivable:

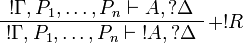
$\AxRule{\oc\Gamma,P_1,\dots,P_n\vdash A,\wn\Delta} \LabelRule{+ \oc R} \UnaRule{\oc\Gamma,P_1,\dots,P_n\vdash \oc{A},\wn\Delta} \DisplayProof$

Proof. $\AxRule{P_1\vdash\oc{P_1}} \AxRule{P_n\vdash\oc{P_n}} \AxRule{\oc\Gamma,P_1,\dots,P_n\vdash A,\wn\Delta} \LabelRule{\oc L} \UnaRule{\oc\Gamma,P_1,\dots,\oc{P_n}\vdash A,\wn\Delta} \UnaRule{\vdots} \LabelRule{\oc L} \UnaRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_n}\vdash A,\wn\Delta} \LabelRule{\oc R} \UnaRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_n}\vdash \oc{A},\wn\Delta} \LabelRule{\rulename{cut}} \BinRule{\oc\Gamma,\oc{P_1},\dots,P_n\vdash \oc{A},\wn\Delta} \UnaRule{\vdots} \LabelRule{\rulename{cut}} \BinRule{\oc\Gamma,P_1,\dots,P_n\vdash \oc{A},\wn\Delta} \DisplayProof$

Revision as of 15:58, 6 March 2009 (view source) Olivier Laurent (Talk \| contribs) (New page: A ''positive formula'' is a formula <math>P</math> such that <math>P\limp\oc P</math> (thus a coalgebra for the comonad <math>\oc</math>). A...)		Revision as of 16:53, 12 March 2009 (view source) Emmanuel Beffara (Talk \| contribs) m (Updated the 'equivalent' link) Newer edit →
Line 1:		Line 1:
−	A ''positive formula'' is a formula <math>P</math> such that <math>P\limp\oc P</math> (thus a [[Wikipedia:F-coalgebra\|coalgebra]] for the [[Wikipedia:Comonad\|comonad]] <math>\oc</math>). As a consequence <math>P</math> and <math>\oc P</math> are [[Sequent calculus#Equivalences and definability\|equivalent]].	+	A ''positive formula'' is a formula <math>P</math> such that <math>P\limp\oc P</math> (thus a [[Wikipedia:F-coalgebra\|coalgebra]] for the [[Wikipedia:Comonad\|comonad]] <math>\oc</math>). As a consequence <math>P</math> and <math>\oc P</math> are [[Sequent calculus#Equivalences\|equivalent]].

	== Positive connectives ==		== Positive connectives ==

Positive formula

Revision as of 16:53, 12 March 2009

Positive connectives

Generalized structural rules

Views

Personal tools

Navigation

Search

Tools