Coherent semantics

Revision as of 22:25, 7 February 2009

Coherent semantics was invented by Girard in the paper The system F, 15 years later. It is a refinement of the former qualitative domains that allows for building an interpretation of system F terms, that is for second order quantifiers.

Coherent semantics is based on the notion of stable functions that was initially proposed by Gérard Berry. Stability is a condition on Scott continuous functions that expresses the determinism of the relation between the output and the input: the typical Scott continuous but non stable function is the parallel or because when the two inputs are both set to true, only one of them is the reason why the result is true but there is no way to determine which one.

Although coherent semantics allowed to solve for the first time the old standing problem of building a denotationnal semantics for polymorphism, one of its main interest is that it also lead Girard to discover the notion of linear function, which rapidly gave rise to linear logic. It is one of the originality of linear logic that its syntax was derived from its semantics.

Preliminary definitions and notations

There are two equivalent definitions of coherence spaces: the first one, coherent spaces as graphs, is the most commonly used and will be our "official" definition in the sequel. The second one, coherent spaces as domains, is however interesting from a historical point of view.

Coherent spaces

As graphs

Definition (Coherent space)

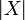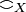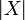A coherent space $X$ is a set of points denoted $\web X$ and called the web of $X$ together with a reflexive and symetric relation $\coh_X$ on $\web X$ called the coherence relation. Coherent spaces are identified with the simple unoriented graphes of their coherence relations.

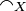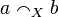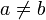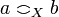The strict coherence relation $\scoh_X$ on $X$ is defined by: $a\scoh_X b$ iff $a\neq b$ and $a\coh_X b$ .

Definition (Clique)

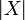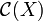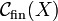A clique of the coherent space $X$ is a set of points in $\web X$ that are pairwise coherent. In other terms a clique is a subgraph of $X$ that is complete. The set of cliques of $X$ is denoted as $\mathcal{C}(X)$ . We will often use the set of finite cliques of $X$ that will be denoted $\mathcal{C}_\mathrm{fin}(X)$ .

As domains

Definition (Coherent space)

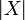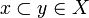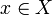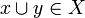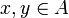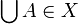A coherent space $X$ is a family of subsets of a set $\web X$ which is closed by subset (if $x\subset y\in X$ then $x\in X$ ) and satisfies the binary compatibility: if $A$ is a family of pairwise compatible elements of $X$ , that is if $x\cup y\in X$ for any $x,y\in A$ , then $\bigcup A\in X$ .

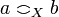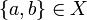When viewed as a set ordered by inclusion a coherent space is particular case of domain. The reader will easily check that one recovers the previous definition by setting $a\coh_X b$ iff $\{a,b\}\in X$ and conversely that the set of cliques of a coherent space in the graph sense is a coherent space in the domain sense. In particular finite cliques of $X$ correspond to compact elements.

Stable functions

From now on we will identify the coherent space (in the graph sense) $X$ with its set of cliques 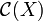$\mathcal{C}(X)$ . Accordingly a function $F$ from $X$ to $Y$ is a function defined on the cliques of $X$ taking values in the cliques of $Y$ .

Definition (Stable function)

Let $X$ and $Y$ be two coherent spaces. A function 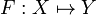$F:X\mapsto Y$ is stable if it satisfies:

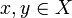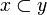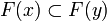it is non decreasing: for any $x,y\in X$ if $x\subset y$ then $F(x)\subset F(y)$ ;
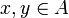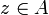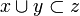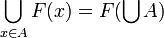it is continuous (in the Scott sense): if $A$ is a directed family of cliques of $X$ , that is if for any $x,y\in A$ there is a $z\in A$ such that $x\cup y\subset z$ , then $\bigcup_{x\in A}F(x) = F(\bigcup A)$ ;
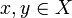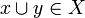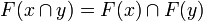it satisfies the stability condition: if $x,y\in X$ are compatible, that is if $x\cup y\in X$ , then $F(x\cap y) = F(x)\cap F(y)$ .

This definition is admitedly not very tractable. An equivalent and most useful caracterisation of stable functions is given by the following theorem.

Theorem

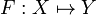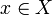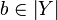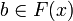Let $F:X\mapsto Y$ be a non-decreasing function from the coherent space $X$ to the coherent space $Y$ . The function $F$ is stable iff it satisfies: for any $x\in X$ , $b\in\web Y$ , if $b\in F(x)$ then there is a finite clique 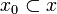$x_0\subset x$ such that:

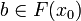$b\in F(x_0)$ ,
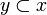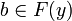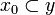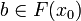for any $y\subset x$ if $b\in F(y)$ then $x_0\subset y$ ( $x 0$ is the minimum sub-clique of $x$ such that $b\in F(x_0)$ ).

Note that the stability condition doesn't depend on the coherent space structure and can be expressed more generally for continuous functions on domains. However the restriction to coherent spaces allows to get an interesting property: the set of stable functions from $X$ to $Y$ may be in turn endowed with a structure of coherent spaces. In categorical terms, the category of coherent spaces with stable functions is closed.

Definition (The space of stable functions)

Let $X$ and $Y$ be coherent spaces. The function space 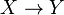$X\rightarrow Y$ is defined by:

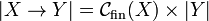$\web{X\rightarrow Y} = \mathcal{C}_{\mathrm{fin}}(X)\times \web Y$ ,
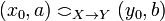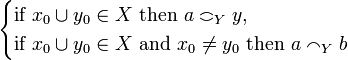$(x_0, a)\coh_{X\rightarrow Y}(y_0, b)$ iff $\begin{cases}\text{if } x_0\cup y_0\in X\text{ then } a\coh_Y y,\\ \text{if } x_0\cup y_0\in X\text{ and } x_0\neq y_0 \text{ then } a\scoh_Y b\end{cases}$ .

Definition (Trace of a stable function)

Let 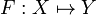$F:X\mapsto Y$ be a function (from the cliques of $X$ to the cliques of $Y$ ). The trace of $F$ is the set:

$Tr(F) = {(x 0, b), x 0$ minimal such that 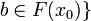$b\in F(x_0)\}$ .

Theorem

If $F$ is stable then $Tr(F)$ is a clique of the function space 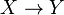$X\rightarrow Y$

In particular the continuity of $F$ entails that if $x 0$ is minimal such that 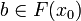$b\in F(x_0)$ , then $x 0$ is finite.

@@ Line 53: / Line 53: @@
 {{Definition|title=The space of stable functions|
-Let <math>X</math> and <math>Y</math> be coherent spaces. The space <math>X\rightarrow Y</math> is defined by:
+Let <math>X</math> and <math>Y</math> be coherent spaces. The function space <math>X\rightarrow Y</math> is defined by:
 * <math>\web{X\rightarrow Y} = \mathcal{C}_{\mathrm{fin}}(X)\times \web Y</math>,
 * <math>(x_0, a)\coh_{X\rightarrow Y}(y_0, b)</math> iff <math>\begin{cases}\text{if } x_0\cup y_0\in X\text{ then } a\coh_Y y,\\
@@ Line 59: / Line 59: @@
 }}
-{{Theorem|
+{{Definition|title=Trace of a stable function|
-Let <math>X</math> and <math>Y</math> be two coherent spaces. We denote by <math>Y^X</math> the set of stable functions from <math>X</math> to <math>Y</math>.
+Let <math>F:X\mapsto Y</math> be a function (from the cliques of <math>X</math> to the cliques of <math>Y</math>). The ''trace'' of <math>F</math> is the set:
+<math>\mathrm{Tr}(F) = \{(x_0, b), x_0</math> minimal such that <math> b\in F(x_0)\}</math>.
 }}
+{{theorem|
+If <math>F</math> is stable then <math>\mathrm{Tr}(F)</math> is a clique of the function space <math>X\rightarrow Y</math>
+}}
+In particular the continuity of <math>F</math> entails that if <math>x_0</math> is minimal such that <math>b\in F(x_0)</math>, then <math>x_0</math> is finite.
 === Linear functions ===

Coherent semantics

Revision as of 22:25, 7 February 2009

Contents

Preliminary definitions and notations

Coherent spaces

As graphs

As domains

Stable functions

Linear functions

Views

Personal tools

Navigation

Search

Tools