Provable formulas
From LLWiki
(Difference between revisions)
(Promotion principles added) |
(→Distributivities: added principles and commutations) |
||
| Line 7: | Line 7: | ||
== Distributivities == |
== Distributivities == |
||
| − | <math>A\tens (B\parr C) \limp (A\tens B)\parr C</math> |
+ | === Standard distributivities === |
<math>A\plus (B\with C) \limp (A\plus B)\with (A\plus C)</math> |
<math>A\plus (B\with C) \limp (A\plus B)\with (A\plus C)</math> |
||
<math>A\tens (B\with C) \limp (A\tens B)\with (A\tens C)</math> |
<math>A\tens (B\with C) \limp (A\tens B)\with (A\tens C)</math> |
||
| + | |||
| + | <math>\exists \xi . (A \with B) \limp (\exists \xi . A) \with (\exists \xi . B)</math> |
||
| + | |||
| + | === Linear distributivities === |
||
| + | |||
| + | <math>A\tens (B\parr C) \limp (A\tens B)\parr C</math> |
||
| + | |||
| + | <math>\exists \xi. (A \parr B) \limp A \parr \exists \xi.B \quad (\xi\notin A)</math> |
||
| + | |||
| + | <math>A \tens \forall \xi.B \limp \forall \xi. (A \tens B) \quad (\xi\notin A)</math> |
||
| + | |||
| + | == Commutations == |
||
| + | |||
| + | <math>\exists \xi . \wn A \limp \wn{\exists \xi . A}</math> |
||
| + | |||
| + | <math>\oc{\forall \xi . A} \limp \forall \xi . \oc A</math> |
||
| + | |||
| + | <math>\wn{\forall \xi . A} \limp \forall \xi . \wn A</math> |
||
| + | |||
| + | <math>\exists \xi . \oc A \limp \oc{\exists \xi . A}</math> |
||
== Factorizations == |
== Factorizations == |
||
Revision as of 19:35, 28 October 2013
This page is a stub and needs more content.
Important provable formulas are given by isomorphisms and by equivalences.
In many of the cases below the converse implication does not hold.
Contents |
Distributivities
Standard distributivities
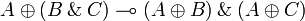
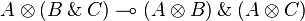
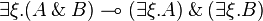
Linear distributivities
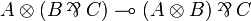
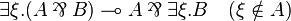
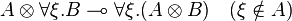
Commutations
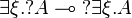
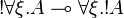
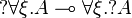
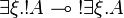
Factorizations
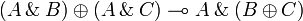
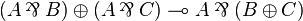
Additive structure
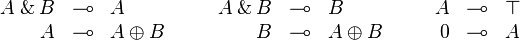
Quantifiers
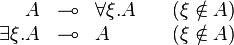
![\begin{array}{rcl}
\forall \xi_1.\forall \xi_2. A &\limp& \forall \xi. A[^\xi/_{\xi_1},^\xi/_{\xi_2}] \\
\exists \xi.A[^\xi/_{\xi_1},^\xi/_{\xi_2}] &\limp& \exists \xi_1. \exists \xi_2.A
\end{array}](/mediawiki/images/math/6/4/d/64db1b58e77150de29a637a18ef888d0.png)
Exponential structure
Provable formulas involving exponential connectives only provide us with the lattice of exponential modalities.

Monoidality of exponentials
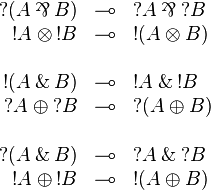
Promotion principles