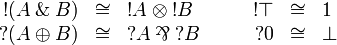Semantics
From LLWiki
(Difference between revisions)
m (notation for isomorphismes \cong instead of \sim) |
Lionel Vaux (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | Linear Logic has numerous semantics some of which are described in details in the next sections. We give here an overview of the common properties that one may find in most of these models. We will denote by <math>A\longrightarrow B</math> the fact that there is a canonical morphism from <math>A</math> to <math>B</math> and by <math>A\sim B</math> the fact that there is a canonical isomorphism between <math>A</math> and <math>B</math>. By "canonical" we mean that these (iso)morphisms are natural transformations. |
+ | Linear Logic has numerous semantics some of which are described in details in the next sections. We give here an overview of the common properties that one may find in most of these models. We will denote by <math>A\longrightarrow B</math> the fact that there is a canonical morphism from <math>A</math> to <math>B</math> and by <math>A\cong B</math> the fact that there is a canonical isomorphism between <math>A</math> and <math>B</math>. By "canonical" we mean that these (iso)morphisms are natural transformations. |
== Linear negation == |
== Linear negation == |
||
Revision as of 14:54, 6 September 2012
Linear Logic has numerous semantics some of which are described in details in the next sections. We give here an overview of the common properties that one may find in most of these models. We will denote by 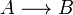 the fact that there is a canonical morphism from A to B and by
the fact that there is a canonical morphism from A to B and by 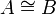 the fact that there is a canonical isomorphism between A and B. By "canonical" we mean that these (iso)morphisms are natural transformations.
the fact that there is a canonical isomorphism between A and B. By "canonical" we mean that these (iso)morphisms are natural transformations.
Contents |
Linear negation
![\begin{array}{rclcrcl}
A\biorth &=& A\\
(A\tens B)\orth &\cong& A\orth\parr B\orth &\quad& \one\orth &\cong& \bot\\
(A\parr B)\orth &\cong& A\orth\tens B\orth &\quad& \bot\orth &\cong& \one\\
(A\with B)\orth &\cong& A\orth\plus B\orth &\quad& \top\orth &\cong& \zero\\
(A\plus B)\orth &\cong& A\orth\with B\orth &\quad& \zero\orth &\cong& \top\\
(\oc A)\orth &\cong& \wn A\orth\\
(\wn A)\orth &\cong& \oc A\orth\\[1ex]
A\limp B &\cong& A\orth\parr B\\
A\limp B &\cong& B\orth\limp A\orth\\
\end{array}](/mediawiki/images/math/9/a/4/9a4031daae652e46533517511236351e.png)
Neutrals
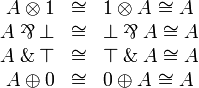
Commutativity
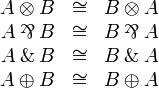
Associativity
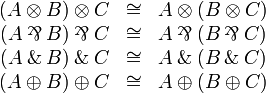
Multiplicative semi-distributivity
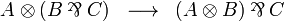
Multiplicative-additive distributivity
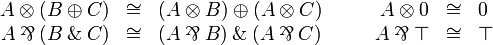
Additive structure
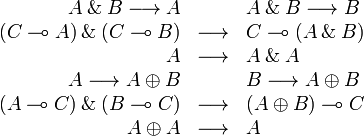
Exponential structure

Monoidality of exponential
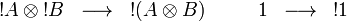
The exponential isomorphism