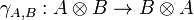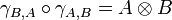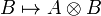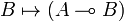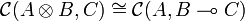Categorical semantics

Revision as of 18:58, 23 March 2009

Constructing denotational models of linear can be a tedious work. Categorical model are useful to identify the fundamental structure of these models, and thus simplify and make more abstract the elaboration of those models.

TODO: why categories? how to extract categorical models? etc.

See ^[1]for a more detailed introduction to category theory.

Modeling IMLL

A model of IMLL is a closed symmetric monoidal category. We recall the definition of these categories below.

Definition (Monoidal category)

A monoidal category 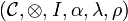$(\mathcal{C},\otimes,I,\alpha,\lambda,\rho)$ is a category 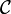$\mathcal{C}$ equipped with

a functor 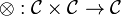$\otimes:\mathcal{C}\times\mathcal{C}\to\mathcal{C}$ called tensor product,
an object $I$ called unit object,
three natural isomorphisms $α$ , $λ$ and $ρ$ , called respectively associator, left unitor and right unitor, whose components are

$\alpha_{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C) \qquad \lambda_A:I\otimes A\to A \qquad \rho_A:A\otimes I\to A$

such that

for every objects $A, B, C, D$ in 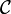$\mathcal{C}$ , the diagram

commutes,

for every objects $A$ and $B$ in 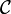$\mathcal{C}$ , the diagrams

commute.

Definition (Braided, symmetric monoidal category)

A braided monoidal category is a category together with a natural isomorphism of components

$\gamma_{A,B}:A\otimes B\to B\otimes A$

called braiding, such that the two diagrams

UNIQ605b9e6874f1a885-math-00000011-QINU

commute for every objects $A$ , $B$ and $C$ .

A symmetric monoidal category is a braided monoidal category in which the braiding satisfies

$\gamma_{B,A}\circ\gamma_{A,B}=A\otimes B$

for every objects $A$ and $B$ .

Definition (Closed monoidal category)

A monoidal category 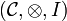$(\mathcal{C},\tens,I)$ is left closed when for every object $A$ , the functor

$B\mapsto A\otimes B$

has a right adjoint, written

$B\mapsto(A\limp B)$

This means that there exists a bijection

$\mathcal{C}(A\tens B, C) \cong \mathcal{C}(A,B\limp C)$

which is natural in $B$ and $C$ . Equivalently, a monoidal category is left closed when it is equipped with a left closed structure, which consists of

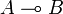an object $A\limp B$ ,
a mo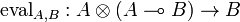rphism $\mathrm{eval}_{A,B}:A\tens (A\limp B)\to B$ , called left evaluation,

for every objects $A$ and $B$ , such that for every morphism 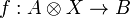$f:A\otimes X\to B$ there exists a unique morphism 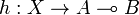$h:X\to A\limp B$ making the diagram Failed to parse (PNG conversion failed; check for correct installation of latex and dvipng (or dvips + gs + convert)):

commute.

Dually, the monoidal category 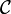$\mathcal{C}$ is right closed when the functor 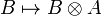$B\mapsto B\otimes A$ admits a right adjoint. The notion of right closed structure can be defined similarly.

In a symmetric monoidal category, a left closed structure induces a right closed structure and conversely, allowing us to simply speak of a closed symmetric monoidal category.

Modeling the additives

Definition (Product)

Definition (Monoid)

Property

Categories with products vs monoidal categories.

Modeling IMALL

Modeling negation

Definition (*-autonomous category)

TODO

References

↑ MacLane, Saunders. Categories for the Working Mathematician.

[0] MacLane, Saunders. Categories for the Working Mathematician.

[1]

@@ Line 39: / Line 39: @@
 for every objects <math>A</math> and <math>B</math>.
 }}
+{{Definition|title=Closed monoidal category|
+A monoidal category <math>(\mathcal{C},\tens,I)</math> is ''left closed'' when for every object <math>A</math>, the functor
+:<math>B\mapsto A\otimes B</math>
+has a right adjoint, written
+:<math>B\mapsto(A\limp B)</math>
+This means that there exists a bijection
+:<math>\mathcal{C}(A\tens B, C) \cong \mathcal{C}(A,B\limp C)</math>
+which is natural in <math>B</math> and <math>C</math>.
+Equivalently, a monoidal category is left closed when it is equipped with a ''left closed structure'', which consists of
+* an object <math>A\limp B</math>,
+* a morphism <math>\mathrm{eval}_{A,B}:A\tens (A\limp B)\to B</math>, called ''left evaluation'',
+for every objects <math>A</math> and <math>B</math>, such that for every morphism <math>f:A\otimes X\to B</math> there exists a unique morphism <math>h:X\to A\limp B</math> making the diagram
+<math>
+</math>
+commute.
+Dually, the monoidal category <math>\mathcal{C}</math> is ''right closed'' when the functor <math>B\mapsto B\otimes A</math> admits a right adjoint. The notion of ''right closed structure'' can be defined similarly.
+}}
+In a symmetric monoidal category, a left closed structure induces a right closed structure and conversely, allowing us to simply speak of a ''closed symmetric monoidal category''.
 == Modeling the additives ==

Categorical semantics

Revision as of 18:58, 23 March 2009

Contents

Modeling IMLL

Modeling the additives

Modeling IMALL

Modeling negation

References

Views

Personal tools

Navigation

Search

Tools