Light linear logics
(→Elementary linear logic) |
(→Elementary linear logic) |
||
| Line 33: | Line 33: | ||
<math>K(0,n)=n, \quad K(k+1,n)=2^{K(k,n)}</math>.<br> |
<math>K(0,n)=n, \quad K(k+1,n)=2^{K(k,n)}</math>.<br> |
||
{{Theorem|If <math>\pi</math> is an ELL proof of depth d, and R is the corresponding ELL proof-net, then R can be reduced to its normal form by cut elimination in at most <math> K(d+1,|\pi|)</math> steps, where <math>|\pi|</math>is the size of <math>\pi</math>.}} |
{{Theorem|If <math>\pi</math> is an ELL proof of depth d, and R is the corresponding ELL proof-net, then R can be reduced to its normal form by cut elimination in at most <math> K(d+1,|\pi|)</math> steps, where <math>|\pi|</math>is the size of <math>\pi</math>.}} |
||
| + | A function f is ''elementary recursive'' |
||
| + | if there exists an integer h and a Turing machine |
||
| + | which computes |
||
| + | f in time bounded by <math>K(h,n)</math>. |
||
Revision as of 18:17, 19 March 2009
Light linear logics are variants of linear logic characterizing complexity classes. They are designed by defining alternative exponential connectives, which induce a complexity bound on the cut-elimination procedure.
Light linear logics are one of the approaches used in implicit computational complexity, the research area studying the computational complexity of programs without referring to external measuring conditions or particular machine models.
Elementary linear logic
We present here the intuitionistic version of elementary linear logic, ELL. Moreover we restrict to the fragment without additive connectives.
The language of formulas is the same one as that of (multiplicative) ILL:
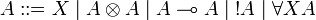
The sequent calculus rules are the same ones as for ILL, except for the rules
dealing with the exponential connectives:
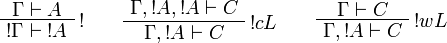
The depth of a derivation π is the maximum number of
 rules in a branch of π.
rules in a branch of π.
We consider the function K(.,.) defined by:
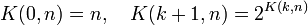 .
.
Theorem
If π is an ELL proof of depth d, and R is the corresponding ELL proof-net, then R can be reduced to its normal form by cut elimination in at most K(d + 1, | π | ) steps, where | π | is the size of π.
A function f is elementary recursive
if there exists an integer h and a Turing machine which computes f in time bounded by K(h,n).