Relational semantics
(New page: == Relational semantics == This is the simplest denotational semantics of linear logic. It consists in interpreting a formula <math>A</math> as a set <math>A^*</math> and a proof <math>\p...) |
(→The category of sets and relations) |
||
| Line 8: | Line 8: | ||
sets |
sets |
||
| − | <math>t\circ s=\set{(a,c)\in X\times Z}{\exists b\in Y\ (a,b)\in s\ \text{and}\ (b,c)\in t}</math>. |
+ | <math>t\circ s=\set{(a,c)\in X\times Z}{\exists b\in Y\ (a,b)\in s\ \text{and}\ (b,c)\in t}</math> |
| + | |||
| + | and the identity morphism is the diagonal relation <math>\mathsf{Id}_X=\set{(a,a)}{a\in X}</math>. |
||
| + | |||
| + | An isomorphism in the category <math>\mathbf{Rel}</math> is a relation which is a bijection, as easily checked. |
||
| + | |||
| + | ==== Monoidal structure ==== |
||
| + | |||
| + | The tensor product is the usual cartesian product <math>X\tens Y=X\times Y</math>. It is a bifunctor: given <math>s_i\in\mathbf{Rel}(X_i,Y_i)</math> (for <math>i=1,2</math>), one sets <math>s_1\tens s_2=\set{((a_1,a_2),(b_1,b_2))}{(a_i,b_i)\in s_i\ \text{for}\ i=1,2}</math>. The unit of this monoidal functor is <math>\one=\{*\}</math> where <math>*</math> is an arbitrary element. |
||
| + | |||
| + | For defining a monoidal category, it is not sufficient to provide the definition of the tensor product functor <math>\tens</math> and its unit <math>\one</math>, one has also to provide natural isomorphisms <math>\lambda_X\in\mathbf{Rel}(\one\tens X,X)</math>, |
||
| + | <math>\rho_X\in\mathbf{Rel}(X\tens\one,X)</math> (left and right neutrality of <math>\one</math> for <math>\tens</math>) and <math>\alpha_{X,Y,Z}\in\mathbf{Rel}((X\tens Y)\tens Z,X\tens(Y\tens Z))</math> (associativity of <math>\tens</math>). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way. |
||
| + | |||
| + | This monoidal category <math>(\mathbf{Rel},\tens,\one,\lambda,\rho)</math> is symmetric, meaning that it is endowed with an additional natural isomorphism <math>\sigma_{X,Y}\in\mathbf{Rel}(X\tens Y,Y\tens X)</math>, also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category) <math>\mathbf{Rel}</math> is the tuple <math>(\mathbf{Rel},\tens,\one,\lambda,\rho,\sigma)</math>. |
||
Revision as of 06:35, 16 March 2009
Relational semantics
This is the simplest denotational semantics of linear logic. It consists in interpreting a formula A as a set A * and a proof π of A as a subset π * of A * .
The category of sets and relations
It is the category 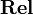 whose objects are sets, and such that
whose objects are sets, and such that 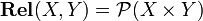 . Composition is the ordinary composition of relations: given
. Composition is the ordinary composition of relations: given 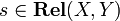 and
and 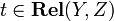 , one
sets
, one
sets
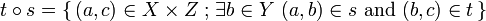
and the identity morphism is the diagonal relation 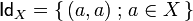 .
.
An isomorphism in the category 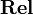 is a relation which is a bijection, as easily checked.
is a relation which is a bijection, as easily checked.
Monoidal structure
The tensor product is the usual cartesian product 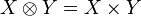 . It is a bifunctor: given
. It is a bifunctor: given 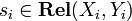 (for i = 1,2), one sets
(for i = 1,2), one sets 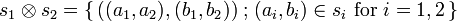 . The unit of this monoidal functor is
. The unit of this monoidal functor is 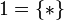 where * is an arbitrary element.
where * is an arbitrary element.
For defining a monoidal category, it is not sufficient to provide the definition of the tensor product functor  and its unit
and its unit 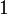 , one has also to provide natural isomorphisms
, one has also to provide natural isomorphisms 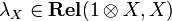 ,
,
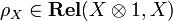 (left and right neutrality of
(left and right neutrality of 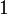 for
for 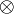 ) and
) and 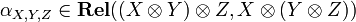 (associativity of
(associativity of 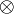 ). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way.
). All these isomorphisms have to satisfy a number of commutations. In the present case, they are defined in the obvious way.
This monoidal category 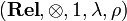 is symmetric, meaning that it is endowed with an additional natural isomorphism
is symmetric, meaning that it is endowed with an additional natural isomorphism 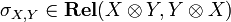 , also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category)
, also subject to some commutations. Here, again, this isomorphism is defined in the obvious way (symmetry of the cartesian product). So, to be precise, the SMCC (symmetric monoidal closed category) 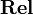 is the tuple
is the tuple 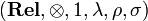 .
.