Coherent semantics

Revision as of 21:32, 4 March 2009

Coherent semantics was invented by Girard in the paper The system F, 15 years later^[1]with the objective of building a denotationnal interpretation of second order intuitionnistic logic (aka polymorphic lambda-calculus).

Coherent semantics is based on the notion of stable functions that was initially proposed by Gérard Berry. Stability is a condition on Scott continuous functions that expresses the determinism of the relation between the output and the input: the typical Scott continuous but non stable function is the parallel or because when the two inputs are both set to true, only one of them is the reason why the result is true but there is no way to determine which one.

A further achievement of coherent semantics was that it allowed to endow the set of stable functions from $X$ to $Y$ with a structure of domain, thus closing the category of coherent spaces and stable functions. However the most interesting point was the discovery of a special class of stable functions, linear functions, which was the first step leading to Linear Logic.

The cartesian closed structure of coherent semantics

There are three equivalent definitions of coherent spaces: the first one, coherent spaces as domains, is interesting from a historical point of view as it emphazises the fact that coherent spaces are particular cases of Scott domains. The second one, coherent spaces as graphs, is the most commonly used and will be our "official" definition in the sequel. The last one, cliqued spaces is a particular example of a more general scheme that one could call "symmetric reducibility"; this scheme is underlying lots of constructions in linear logic such as phase semantics or the proof of strong normalisation for proof-nets.

Coherent spaces

A coherent space $X$ is a collection of subsets of a set 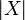$\web X$ satisfying some conditions that will be detailed shortly. The elements of $X$ are called the cliques of $X$ (for reasons that will be made clear in a few lines). The set 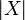$\web X$ is called the web of $X$ and its elements are called the points of $X$ ; thus a clique is a set of points. Note that the terminology is a bit ambiguous as the points of $X$ are the elements of the web of $X$ , not the elements of $X$ .

The definitions below give three equivalent conditions that have to be satisfied by the cliques of a coherent space.

As domains

The cliques of $X$ have to satisfy:

subset closure: if 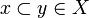$x\subset y\in X$ then $x\in X$ ,
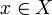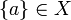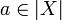singletons: $\{a\}\in X$ for $a\in\web X$ .
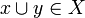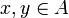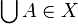binary compatibility: if $A$ is a family of pairwise compatible cliques of $X$ , that is if $x\cup y\in X$ for any $x,y\in A$ , then $\bigcup A\in X$ .

A coherent space is thus ordered by inclusion; one easily checks that it is a domain. In particular finite cliques of $X$ correspond to compact elements.

As graphs

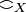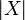There is a reflexive and symetric relation $\coh_X$ on $\web X$ (the coherence relation) such that any subset $x$ of 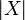$\web X$ is a clique of $X$ iff 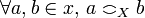$\forall a,b\in x,\, a\coh_X b$ . In other terms $X$ is the set of complete subgraphs of the simple unoriented graph of the 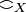$\coh_X$ relation; this is the reason why elements of $X$ are called cliques.

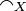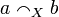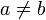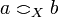The strict coherence relation $\scoh_X$ on $X$ is defined by: $a\scoh_X b$ iff $a\neq b$ and $a\coh_X b$ .

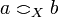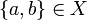A coherent space in the domain sense is seen to be a coherent space in the graph sense by setting $a\coh_X b$ iff $\{a,b\}\in X$ ; conversely one can check that cliques in the graph sense are subset closed and satisfy the binary compatibility condition.

A coherent space is completely determined by its web and its coherence relation, or equivalently by its web and its strict coherence.

As cliqued spaces

Definition (Duality)

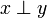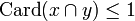Let $x$ and $y$ be two sets. We will say that they are dual, written $x\perp y$ if their intersection contains at most one element: $\mathrm{Card}(x\cap y)\leq 1$ .

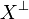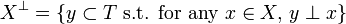
Let $T$ be a set and $X$ be a family of subsets of $T$ . We define the dual of $X$ to be the collection $X\orth$ of subsets of $T$ that are dual to all elements of $X$ : $X\orth = \{y\subset T \text{ s.t. for any } x\in X,\, y\perp x\}$

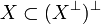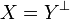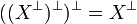Given such a collection $X$ of subsets of $T$ one sees that we have $X\subset (X\orth)\orth$ . The reverse inclusion is not true in general, however it holds in the case where $X=Y\orth$ for some collection $Y$ of subsets of $T$ . In other terms we always have $((X\orth)\orth)\orth = X\orth$ .

From now on we will denote 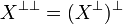$X\biorth = (X\orth)\orth$ .

Given these definitions, the last way to express the conditions on the cliques of a coherent space $X$ is simply to say that we must have 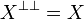$X\biorth = X$ .

Let $X$ be a cliqued space and define a relation on 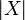$\web X$ by setting 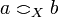$a\coh_X b$ iff there is 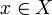$x\in X$ such that 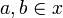$a, b\in x$ . This relation is obviously symetric; it is also reflexive because all singletons belong to $X$ : if 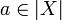$a\in \web X$ then ${a}$ is dual to any element of 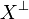$X\orth$ (actually ${a}$ is dual to any subset of 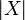$\web X$ ), thus ${a}$ is in 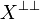$X\biorth$ , thus in $X$ .

Let 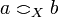$a\coh_X b$ . Then 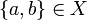$\{a,b\}\in X$ ; indeed there is an 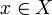$x\in X$ such that 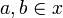$a, b\in x$ . This $x$ is dual to any 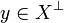$y\in X\orth$ , that is meets any 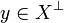$y\in X\orth$ in a most one point. Since 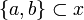$\{a,b\}\subset x$ this is also true of ${a, b}$ , so that ${a, b}$ is in 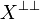$X\biorth$ thus in $X$ . Now let $x$ be a clique for 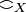$\coh_X$ and $y$ be an element of 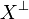$X\orth$ . 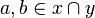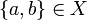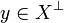Suppose $a, b\in x\cap y$ , then since $a$ and $b$ are coherent (by hypothesis on $x$ ) we have $\{a,b\}\in X$ and since $y\in X\orth$ we must have that ${a, b}$ and $y$ meet in at most one point. Thus $a = b$ and we have shown that $x$ and $y$ are dual. Since $y$ was arbitrary this means that $x$ is in 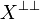$X\biorth$ , thus in $X$ . Finally we get that any set of pairwise coherent points of $X$ is in $X$ . Conversely given 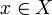$x\in X$ its points are obviously pairwise coherent so eventually we get that $X$ is a coherent space in the graph sense.

Conversely given a coherent space $X$ in the graph sense, one can check that it is a cliqued space. Call anticlique a set 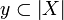$y\subset \web X$ of pairwise incoherent points: for all $a, b$ in $y$ , if 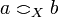$a\coh_X b$ then $a = b$ . Any anticlique intersects any clique in at most one point: let $x$ be a clique and $y$ be an anticlique, then if 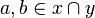$a,b\in x\cap y$ , since 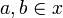$a, b\in x$ we have 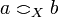$a\coh_X b$ and since $y$ is an anticlique we have $a = b$ .

Thus the collection of anticliques of $X$ is the dual 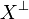$X\orth$ of $X$ . Note that the incoherence relation defined above is reflexive and symetric, so that 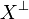$X\orth$ is a coherent space in the graph sense. Thus we can do for 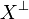$X\orth$ exactly what we've just done for $X$ and consider the anti-anticliques, that is the anticliques for the incoherent relation which are the cliques for the in-incoherent relation. It is not difficult to see that this in-incoherence relation is just the coherence relation we started with; we thus obtain that 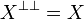$X\biorth = X$ , so that $X$ is a cliqued space.

Stable functions

Definition (Stable function)

Let $X$ and $Y$ be two coherent spaces. A function 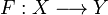$F:X\longrightarrow Y$ is stable if it satisfies:

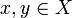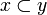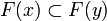it is non decreasing: for any $x,y\in X$ if $x\subset y$ then $F(x)\subset F(y)$ ;
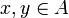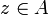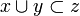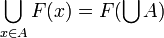it is continuous (in the Scott sense): if $A$ is a directed family of cliques of $X$ , that is if for any $x,y\in A$ there is a $z\in A$ such that $x\cup y\subset z$ , then $\bigcup_{x\in A}F(x) = F(\bigcup A)$ ;
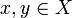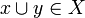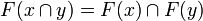it satisfies the stability condition: if $x,y\in X$ are compatible, that is if $x\cup y\in X$ , then $F(x\cap y) = F(x)\cap F(y)$ .

This definition is admitedly not very tractable. An equivalent and most useful caracterisation of stable functions is given by the following theorem.

Theorem

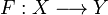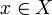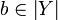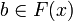Let $F:X\longrightarrow Y$ be a non-decreasing function from the coherent space $X$ to the coherent space $Y$ . The function $F$ is stable iff it satisfies: for any $x\in X$ , $b\in\web Y$ , if $b\in F(x)$ then there is a finite clique 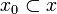$x_0\subset x$ such that:

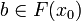$b\in F(x_0)$ ,
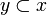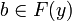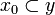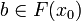for any $y\subset x$ if $b\in F(y)$ then $x_0\subset y$ ( $x 0$ is the minimum sub-clique of $x$ such that $b\in F(x_0)$ ).

Note that the stability condition doesn't depend on the coherent space structure and can be expressed more generally for continuous functions on domains. However, as mentionned in the introduction, the restriction to coherent spaces allows to endow the set of stable functions from $X$ to $Y$ with a structure of coherent space.

Definition (The space of stable functions)

Let $X$ and $Y$ be coherent spaces. We denote by $X fin$ the set of finite cliques of $X$ . The function space 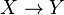$X\imp Y$ is defined by:

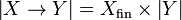$\web{X\imp Y} = X_{\mathrm{fin}}\times \web Y$ ,
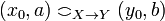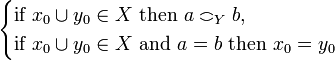$(x_0, a)\coh_{X\imp Y}(y_0, b)$ iff $\begin{cases}\text{if } x_0\cup y_0\in X\text{ then } a\coh_Y b,\\ \text{if } x_0\cup y_0\in X\text{ and } a = b\text{ then } x_0 = y_0\end{cases}$ .

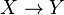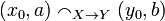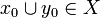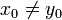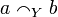One could equivalently define the strict coherence relation on $X\imp Y$ by: $(x_0,a)\scoh_{X\imp Y}(y_0, b)$ iff $x_0\cup y_0\in X$ and $x_0\neq y_0$ entails that $a\scoh_Y b$ .

Definition (Trace of a stable function)

Let 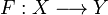$F:X\longrightarrow Y$ be a function. The trace of $F$ is the set:

$Tr(F) = {(x 0, b), x 0$ minimal such that 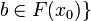$b\in F(x_0)\}$ .

Theorem

$F$ is stable iff $Tr(F)$ is a clique of the function space 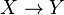$X\imp Y$

In particular the continuity of $F$ entails that if $x 0$ is minimal such that 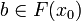$b\in F(x_0)$ , then $x 0$ is finite.

Definition (The evaluation function)

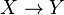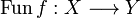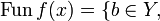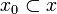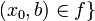Let $f$ be a clique in $X\imp Y$ . We define a function $\mathrm{Fun}\,f:X\longrightarrow Y$ by: $\mathrm{Fun}\,f(x) = \{b\in Y,$ there is $x_0\subset x$ such that $(x_0, b)\in f\}$ .

Theorem (Closure)

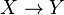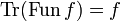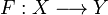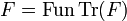If $f$ is a clique of the function space $X\imp Y$ then we have $\mathrm{Tr}(\mathrm{Fun}\,f) = f$ . Conversely if $F:X\longrightarrow Y$ is a stable function then we have $F = \mathrm{Fun}\,\mathrm{Tr}(F)$ .

Cartesian product

Definition (Cartesian product)

Let $X 1$ and $X 2$ be two coherent spaces. Their cartesian products 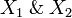$X_1\with X_2$ is the coherent space defined by:

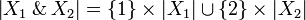the web is the disjoint union of the webs: $\web{X_1\with X_2} = \{1\}\times\web{X_1}\cup \{2\}\times\web{X_2}$ ;
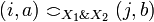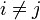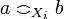the coherence relation is the serie composition of the relations on $X 1$ and $X 2$ : $(i, a)\coh_{X_1\with X_2}(j, b)$ iff $i\neq j$ or $i = j$ and $a\coh_{X_i} b$ .

This definition is just the way to put a coherent space structure on the cartesian product. Indeed one easily shows the

Theorem

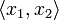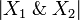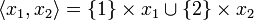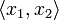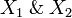Given cliques $x 1$ and $x 2$ in $X 1$ and $X 2$ , we define the subset $\langle x_1, x_2\rangle$ of $\web{X_1\with X_2}$ by: $\langle x_1, x_2\rangle = \{1\}\times x_1\cup \{2\}\times x_2$ . Then $\langle x_1, x_2\rangle$ is a clique in $X_1\with X_2$ .

Conversely, given a clique 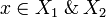$x\in X_1\with X_2$ , for $i = 1,2$ we define 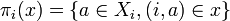$\pi_i(x) = \{a\in X_i, (i, a)\in x\}$ . Then $π i (x)$ is a clique in $X i$ and the function 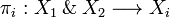$\pi_i:X_1\with X_2\longrightarrow X_i$ is stable.

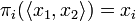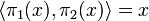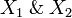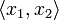Furthemore these two operations are inverse of each other: $\pi_i(\langle x_1, x_2\rangle) = x_i$ and $\langle\pi_1(x), \pi_2(x)\rangle = x$ . In particular any clique in $X_1\with X_2$ is of the form $\langle x_1, x_2\rangle$ .

Altogether the results above (and a few other more that we shall leave to the reader) allow to get:

Theorem

The category of coherent spaces and stable functions is cartesian closed.

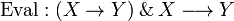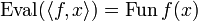In particular this means that if we define $\mathrm{Eval}:(X\imp Y)\with X\longrightarrow Y$ by: $\mathrm{Eval}(\langle f, x\rangle) = \mathrm{Fun}\,f(x)$ then $Eval$ is stable.

The monoidal structure of coherent semantics

Linear functions

Definition (Linear function)

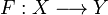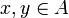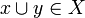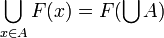A function $F:X\longrightarrow Y$ is linear if it is stable and furthemore satisfies: for any family $A$ of pairwise compatible cliques of $X$ , that is such that for any $x, y\in A$ , $x\cup y\in X$ , we have $\bigcup_{x\in A}F(x) = F(\bigcup A)$ .

In particular if we take $A$ to be the empty family, then we have 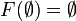$F(\emptyset) = \emptyset$ .

The condition for linearity is quite similar to the condition for Scott continuity, except that we dropped the constraint that $A$ is directed. Linearity is therefore much stronger than stability: most stable functions are not linear.

As with stable function we have an equivalent and much more tractable caracterisation of linear function:

Theorem

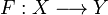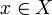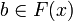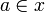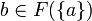Let $F:X\longrightarrow Y$ be a continuous function. Then $F$ is linear iff it satisfies: for any clique $x\in X$ and any $b\in F(x)$ there is a unique $a\in x$ such that $b\in F(\{a\})$ .

Just as the caracterisation theorem for stable functions allowed us to build the coherent space of stable functions, this theorem will help us to endow the set of linear maps with a structure of coherent space.

Definition (The linear functions space)

Let $X$ and $Y$ be coherent spaces. The linear function space 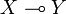$X\limp Y$ is defined by:

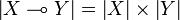$\web{X\limp Y} = \web X\times \web Y$ ,
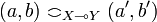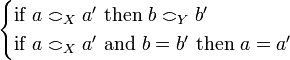
$(a,b)\coh_{X\limp Y}(a', b')$ iff $\begin{cases}\text{if }a\coh_X a'\text{ then } b\coh_Y b'\\ \text{if }a\coh_X a' \text{ and }b=b'\text{ then }a=a'\end{cases}$

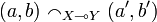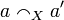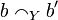Equivalently one could define the strict coherence to be: $(a,b)\scoh_{X\limp Y}(a',b')$ iff $a\scoh_X a'$ entails $b\scoh_Y b'$ .

Definition (Linear trace)

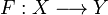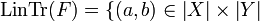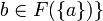Let $F:X\longrightarrow Y$ be a function. The linear trace of $F$ denoted as $LinTr(F)$ is the set: $\mathrm{LinTr}(F) = \{(a, b)\in\web X\times\web Y$ such that $b\in F(\{a\})\}$ .

Theorem

If $F$ is linear then $LinTr(F)$ is a clique of 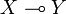$X\limp Y$ .

Definition (Evaluation of linear function)

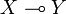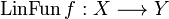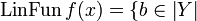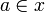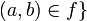Let $f$ be a clique of $X\limp Y$ . We define the function $\mathrm{LinFun}\,f:X\longrightarrow Y$ by: $\mathrm{LinFun}\,f(x) = \{b\in\web Y$ such that there is an $a\in x$ satisfying $(a,b)\in f\}$ .

Theorem (Linear closure)

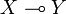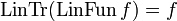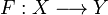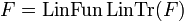Let $f$ be a clique in $X\limp Y$ . Then we have $\mathrm{LinTr}(\mathrm{LinFun}\, f) = f$ . Conversely if $F:X\longrightarrow Y$ is linear then we have $F = \mathrm{LinFun}\,\mathrm{LinTr}(F)$ .

It remains to define a tensor product and we will get that the category of coherent spaces with linear functions is monoidal symetric (it is actually *-autonomous).

Tensor product

Definition (Tensor product)

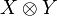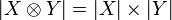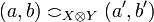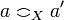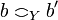Let $X$ and $Y$ be coherent spaces. Their tensor product $X\tens Y$ is defined by: $\web{X\tens Y} = \web X\times\web Y$ and $(a,b)\coh_{X\tens Y}(a',b')$ iff $a\coh_X a'$ and $b\coh_Y b'$ .

Theorem

The category of coherent spaces with linear maps and tensor product is monoidal symetric closed.

The closedness is a consequence of the existence of the linear isomorphism:

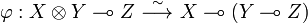
$\varphi:X\tens Y\limp Z\ \stackrel{\sim}{\longrightarrow}\ X\limp(Y\limp Z)$

that is defined by its linear trace: 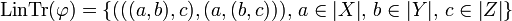$\mathrm{LinTr}(\varphi) = \{(((a, b), c), (a, (b, c))),\, a\in\web X,\, b\in \web Y,\, c\in\web Z\}$ .

Linear negation

Definition (Linear negation)

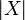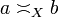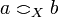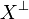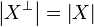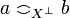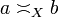Let $X$ be a coherent space. We define the incoherence relation on $\web X$ by: $a\incoh_X b$ iff $a\coh_X b$ entails $a = b$ . The incoherence relation is reflexive and symetric; we call dual or linear negation of $X$ the associated coherent space denoted $X\orth$ , thus defined by: $\web{X\orth} = \web X$ and $a\coh_{X\orth} b$ iff $a\incoh_X b$ .

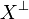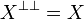The cliques of $X\orth$ are called the anticliques of $X$ . As seen in the section on cliqued spaces we have $X\biorth=X$ .

Theorem

The category of coherent spaces with linear maps, tensor product and linear negation is *-autonomous.

This is in particular consequence of the existence of the isomorphism:

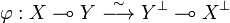
$\varphi:X\limp Y\ \stackrel{\sim}{\longrightarrow}\ Y\orth\limp X\orth$

defined by its linear trace: 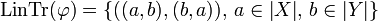$\mathrm{LinTr}(\varphi) = \{((a, b), (b, a)),\, a\in\web X,\, b\in\web Y\}$ .

Exponentials

In linear algebra, bilinear maps may be factorized through the tensor product. Similarly there is a coherent space 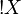$\oc X$ that allows to factorize stable functions through linear functions.

Definition (Of course)

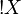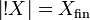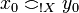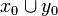Let $X$ be a coherent space; recall that $X fin$ denotes the set of finite cliques of $X$ . We define the space $\oc X$ (read of course $X$ ) by: $\web{\oc X} = X_{\mathrm{fin}}$ and $x_0\coh_{\oc X}y_0$ iff $x_0\cup y_0$ is a clique of $X$ .

Theorem

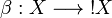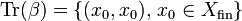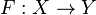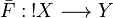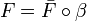Let $X$ be a coherent space. Denote by $\beta:X\longrightarrow \oc X$ the stable function whose trace is: $\mathrm{Tr}(\beta) = \{(x_0, x_0),\, x_0\in X_{\mathrm{fin}}\}$ . Then for any coherent space $Y$ and any stable function $F: X\imp Y$ there is a unique linear function $\bar F:\oc X\longrightarrow Y$ such that $F = \bar F\circ \beta$ .

Furthermore we have 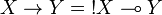$X\imp Y = \oc X\limp Y$ .

References

↑ Girard, Jean-Yves. The System F of Variable Types, Fifteen Years Later. Theoretical Computer Science. Volume 45, Issue 2, pp. 159-192, doi:10.1016/0304-3975(86)90044-7, 1986.

[0] Girard, Jean-Yves. The System F of Variable Types, Fifteen Years Later. Theoretical Computer Science. Volume 45, Issue 2, pp. 159-192, doi:10.1016/0304-3975(86)90044-7, 1986.

[1]

@@ Line 47: / Line 47: @@
 From now on we will denote <math>X\biorth = (X\orth)\orth</math>.
-Given these definitions, the last way to express the conditions on the cliques of <math>X</math> is simply to say that we must have <math>X\biorth = X</math>.
+Given these definitions, the last way to express the conditions on the cliques of a coherent space <math>X</math> is simply to say that we must have <math>X\biorth = X</math>.
 Let <math>X</math> be a cliqued space and define a relation on <math>\web X</math> by setting <math>a\coh_X b</math> iff there is <math>x\in X</math> such that <math>a, b\in x</math>. This relation is obviously symetric; it is also reflexive because all singletons belong to <math>X</math>: if <math>a\in \web X</math> then <math>\{a\}</math> is dual to any element of <math>X\orth</math> (actually <math>\{a\}</math> is dual to any subset of <math>\web X</math>), thus <math>\{a\}</math> is in <math>X\biorth</math>, thus in <math>X</math>.
@@ Line 60: / Line 60: @@
 {{Definition|title=Stable function|
-Let <math>X</math> and <math>Y</math> be two coherent spaces. A function <math>F:X\mapsto Y</math> is ''stable'' if it satisfies:
+Let <math>X</math> and <math>Y</math> be two coherent spaces. A function <math>F:X\longrightarrow Y</math> is ''stable'' if it satisfies:
 * it is non decreasing: for any <math>x,y\in X</math> if <math>x\subset y</math> then <math>F(x)\subset F(y)</math>;
 * it is continuous (in the Scott sense): if <math>A</math> is a directed family of cliques of <math>X</math>, that is if for any <math>x,y\in A</math> there is a <math>z\in A</math> such that <math>x\cup y\subset z</math>, then <math>\bigcup_{x\in A}F(x) = F(\bigcup A)</math>;
@@ Line 69: / Line 69: @@
 {{Theorem|
-Let <math>F:X\mapsto Y</math> be a non-decreasing function from the coherent space <math>X</math> to the coherent space <math>Y</math>. The function <math>F</math> is stable iff it satisfies: for any <math>x\in X</math>, <math>b\in\web Y</math>, if <math>b\in F(x)</math> then there is a finite clique <math>x_0\subset x</math> such that:
+Let <math>F:X\longrightarrow Y</math> be a non-decreasing function from the coherent space <math>X</math> to the coherent space <math>Y</math>. The function <math>F</math> is stable iff it satisfies: for any <math>x\in X</math>, <math>b\in\web Y</math>, if <math>b\in F(x)</math> then there is a finite clique <math>x_0\subset x</math> such that:
 * <math>b\in F(x_0)</math>,
 * for any <math>y\subset x</math> if <math>b\in F(y)</math> then <math>x_0\subset y</math> (<math>x_0</math> is ''the'' minimum sub-clique of <math>x</math> such that <math>b\in F(x_0)</math>).
@@ Line 77: / Line 77: @@
 {{Definition|title=The space of stable functions|
-Let <math>X</math> and <math>Y</math> be coherent spaces. We denote by <math>X_{\mathrm{fin}}</math> the set of ''finite'' cliques of <math>X</math>. The function space <math>X\rightarrow Y</math> is defined by:
+Let <math>X</math> and <math>Y</math> be coherent spaces. We denote by <math>X_{\mathrm{fin}}</math> the set of ''finite'' cliques of <math>X</math>. The function space <math>X\imp Y</math> is defined by:
-* <math>\web{X\rightarrow Y} = X_{\mathrm{fin}}\times \web Y</math>,
+* <math>\web{X\imp Y} = X_{\mathrm{fin}}\times \web Y</math>,
-* <math>(x_0, a)\coh_{X\rightarrow Y}(y_0, b)</math> iff <math>\begin{cases}\text{if } x_0\cup y_0\in X\text{ then } a\coh_Y b,\\
+* <math>(x_0, a)\coh_{X\imp Y}(y_0, b)</math> iff <math>\begin{cases}\text{if } x_0\cup y_0\in X\text{ then } a\coh_Y b,\\
                                                                             \text{if } x_0\cup y_0\in X\text{ and } a = b\text{ then } x_0 = y_0\end{cases}</math>.
 }}
-One could equivalently define the strict coherence relation on <math>X\rightarrow Y</math> by: <math>(x_0,a)\scoh_{X\rightarrow Y}(y_0, b)</math> iff <math>x_0\cup y_0\in X</math> and <math>x_0\neq y_0</math> entails that <math>a\scoh_Y b</math>.
+One could equivalently define the strict coherence relation on <math>X\imp Y</math> by: <math>(x_0,a)\scoh_{X\imp Y}(y_0, b)</math> iff <math>x_0\cup y_0\in X</math> and <math>x_0\neq y_0</math> entails that <math>a\scoh_Y b</math>.
 {{Definition|title=Trace of a stable function|
-Let <math>F:X\mapsto Y</math> be a function. The ''trace'' of <math>F</math> is the set:
+Let <math>F:X\longrightarrow Y</math> be a function. The ''trace'' of <math>F</math> is the set:
 <math>\mathrm{Tr}(F) = \{(x_0, b), x_0</math> minimal such that <math> b\in F(x_0)\}</math>.
@@ Line 92: / Line 92: @@
 {{theorem|
-<math>F</math> is stable iff <math>\mathrm{Tr}(F)</math> is a clique of the function space <math>X\rightarrow Y</math>
+<math>F</math> is stable iff <math>\mathrm{Tr}(F)</math> is a clique of the function space <math>X\imp Y</math>
 }}
@@ Line 98: / Line 98: @@
 {{Definition|title=The evaluation function|
-Let <math>f</math> be a clique in <math>X\rightarrow Y</math>. We define a function <math>\mathrm{Fun}\,f:X\mapsto Y</math> by: <math>\mathrm{Fun}\,f(x) = \{b\in Y,</math> there is <math>x_0\subset x</math> such that <math>(x_0, b)\in f\}</math>.
+Let <math>f</math> be a clique in <math>X\imp Y</math>. We define a function <math>\mathrm{Fun}\,f:X\longrightarrow Y</math> by: <math>\mathrm{Fun}\,f(x) = \{b\in Y,</math> there is <math>x_0\subset x</math> such that <math>(x_0, b)\in f\}</math>.
 }}
 {{Theorem|title=Closure|
-If <math>f</math> is a clique of the function space <math>X\rightarrow Y</math> then we have <math>\mathrm{Tr}(\mathrm{Fun}\,f) = f</math>. Conversely if <math>F:X\mapsto Y</math> is a stable function then we have <math>F = \mathrm{Fun}\,\mathrm{Tr}(F)</math>.
+If <math>f</math> is a clique of the function space <math>X\imp Y</math> then we have <math>\mathrm{Tr}(\mathrm{Fun}\,f) = f</math>. Conversely if <math>F:X\longrightarrow Y</math> is a stable function then we have <math>F = \mathrm{Fun}\,\mathrm{Tr}(F)</math>.
 }}
@@ Line 118: / Line 118: @@
 Given cliques <math>x_1</math> and <math>x_2</math> in <math>X_1</math> and <math>X_2</math>, we define the subset <math>\langle x_1, x_2\rangle</math> of <math>\web{X_1\with X_2}</math> by: <math>\langle x_1, x_2\rangle = \{1\}\times x_1\cup \{2\}\times x_2</math>. Then <math>\langle x_1, x_2\rangle</math> is a clique in <math>X_1\with X_2</math>.
-Conversely, given a clique <math>x\in X_1\with X_2</math>, for <math>i=1,2</math> we define <math>\pi_i(x) = \{a\in X_i, (i, a)\in x\}</math>. Then <math>\pi_i(x)</math> is a clique in <math>X_i</math> and the function <math>\pi_i:X_1\with X_2\mapsto X_i</math> is stable.
+Conversely, given a clique <math>x\in X_1\with X_2</math>, for <math>i=1,2</math> we define <math>\pi_i(x) = \{a\in X_i, (i, a)\in x\}</math>. Then <math>\pi_i(x)</math> is a clique in <math>X_i</math> and the function <math>\pi_i:X_1\with X_2\longrightarrow X_i</math> is stable.
 Furthemore these two operations are inverse of each other: <math>\pi_i(\langle x_1, x_2\rangle) = x_i</math> and <math>\langle\pi_1(x), \pi_2(x)\rangle = x</math>. In particular any clique in <math>X_1\with X_2</math> is of the form <math>\langle x_1, x_2\rangle</math>.
@@ Line 129: / Line 129: @@
 }}
-In particular this means that if we define <math>\mathrm{Eval}:(X\rightarrow Y)\with X\mapsto Y</math> by: <math>\mathrm{Eval}(\langle f, x\rangle) = \mathrm{Fun}\,f(x)</math> then <math>\mathrm{Eval}</math> is stable.
+In particular this means that if we define <math>\mathrm{Eval}:(X\imp Y)\with X\longrightarrow Y</math> by: <math>\mathrm{Eval}(\langle f, x\rangle) = \mathrm{Fun}\,f(x)</math> then <math>\mathrm{Eval}</math> is stable.
 == The monoidal structure of coherent semantics ==
@@ Line 136: / Line 136: @@
 {{Definition|title=Linear function|
-A function <math>F:X\mapsto Y</math> is ''linear'' if it is stable and furthemore satisfies: for any family <math>A</math> of pairwise compatible cliques of <math>X</math>, that is such that for any <math>x, y\in A</math>, <math>x\cup y\in X</math>, we have <math>\bigcup_{x\in A}F(x) = F(\bigcup A)</math>.
+A function <math>F:X\longrightarrow Y</math> is ''linear'' if it is stable and furthemore satisfies: for any family <math>A</math> of pairwise compatible cliques of <math>X</math>, that is such that for any <math>x, y\in A</math>, <math>x\cup y\in X</math>, we have <math>\bigcup_{x\in A}F(x) = F(\bigcup A)</math>.
 }}
@@ Line 146: / Line 146: @@
 {{Theorem|
-Let <math>F:X\mapsto Y</math> be a continuous function. Then <math>F</math> is linear iff it satisfies: for any clique <math>x\in X</math> and any <math>b\in F(x)</math> there is a unique <math>a\in x</math> such that <math>b\in F(\{a\})</math>.
+Let <math>F:X\longrightarrow Y</math> be a continuous function. Then <math>F</math> is linear iff it satisfies: for any clique <math>x\in X</math> and any <math>b\in F(x)</math> there is a unique <math>a\in x</math> such that <math>b\in F(\{a\})</math>.
 }}
@@ Line 161: / Line 161: @@
 {{Definition|title=Linear trace|
-Let <math>F:X\mapsto Y</math> be a function. The ''linear trace'' of <math>F</math> denoted as <math>\mathrm{LinTr}(F)</math> is the set: <math>\mathrm{LinTr}(F) = \{(a, b)\in\web X\times\web Y</math> such that <math>b\in F(\{a\})\}</math>.
+Let <math>F:X\longrightarrow Y</math> be a function. The ''linear trace'' of <math>F</math> denoted as <math>\mathrm{LinTr}(F)</math> is the set: <math>\mathrm{LinTr}(F) = \{(a, b)\in\web X\times\web Y</math> such that <math>b\in F(\{a\})\}</math>.
 }}
@@ Line 169: / Line 169: @@
 {{Definition|title=Evaluation of linear function|
-Let <math>f</math> be a clique of <math>X\limp Y</math>. We define the function <math>\mathrm{LinFun}\,f:X\mapsto Y</math> by: <math>\mathrm{LinFun}\,f(x) = \{b\in\web Y</math> such that there is an <math>a\in x</math> satisfying <math>(a,b)\in f\}</math>.
+Let <math>f</math> be a clique of <math>X\limp Y</math>. We define the function <math>\mathrm{LinFun}\,f:X\longrightarrow Y</math> by: <math>\mathrm{LinFun}\,f(x) = \{b\in\web Y</math> such that there is an <math>a\in x</math> satisfying <math>(a,b)\in f\}</math>.
 }}
 {{Theorem|title=Linear closure|
-Let <math>f</math> be a clique in <math>X\limp Y</math>. Then we have <math>\mathrm{LinTr}(\mathrm{LinFun}\, f) = f</math>. Conversely if <math>F:X\mapsto Y</math> is linear then we have <math>F = \mathrm{LinFun}\,\mathrm{LinTr}(F)</math>.
+Let <math>f</math> be a clique in <math>X\limp Y</math>. Then we have <math>\mathrm{LinTr}(\mathrm{LinFun}\, f) = f</math>. Conversely if <math>F:X\longrightarrow Y</math> is linear then we have <math>F = \mathrm{LinFun}\,\mathrm{LinTr}(F)</math>.
 }}
@@ Line 190: / Line 190: @@
 The closedness is a consequence of the existence of the linear isomorphism:
-<math>\varphi:X\tens Y\limp Z\ \stackrel{\sim}{\rightarrow}\ X\limp(Y\limp Z)</math>
+<math>\varphi:X\tens Y\limp Z\ \stackrel{\sim}{\longrightarrow}\ X\limp(Y\limp Z)</math>
 that is defined by its linear trace: <math>\mathrm{LinTr}(\varphi) = \{(((a, b), c), (a, (b, c))),\, a\in\web X,\, b\in \web Y,\, c\in\web Z\}</math>.
@@ Line 208: / Line 208: @@
 This is in particular consequence of the existence of the isomorphism:
-<math>\varphi:X\limp Y\ \stackrel{\sim}{\rightarrow}\ Y\orth\limp X\orth</math>
+<math>\varphi:X\limp Y\ \stackrel{\sim}{\longrightarrow}\ Y\orth\limp X\orth</math>
 defined by its linear trace: <math>\mathrm{LinTr}(\varphi) = \{((a, b), (b, a)),\, a\in\web X,\, b\in\web Y\}</math>.
@@ Line 222: / Line 222: @@
 {{Theorem|
-Let <math>X</math> be a coherent space. Denote by <math>\beta:X\rightarrow \oc X</math> the stable function whose trace is: <math>\mathrm{Tr}(\beta) = \{(x_0, x_0),\, x_0\in X_{\mathrm{fin}}\}</math>. Then for any coherent space <math>Y</math> and any stable function <math>F: X\rightarrow Y</math> there is a unique ''linear'' function <math>\bar F:\oc X\rightarrow Y</math> such that <math>F = \bar F\circ \beta</math>.
+Let <math>X</math> be a coherent space. Denote by <math>\beta:X\longrightarrow \oc X</math> the stable function whose trace is: <math>\mathrm{Tr}(\beta) = \{(x_0, x_0),\, x_0\in X_{\mathrm{fin}}\}</math>. Then for any coherent space <math>Y</math> and any stable function <math>F: X\imp Y</math> there is a unique ''linear'' function <math>\bar F:\oc X\longrightarrow Y</math> such that <math>F = \bar F\circ \beta</math>.
-Furthermore we have <math>X\rightarrow Y = \oc X\limp Y</math>.
+Furthermore we have <math>X\imp Y = \oc X\limp Y</math>.
 }}

Coherent semantics

Revision as of 21:32, 4 March 2009

Contents

The cartesian closed structure of coherent semantics

Coherent spaces

As domains

As graphs

As cliqued spaces

Stable functions

Cartesian product

The monoidal structure of coherent semantics

Linear functions

Tensor product

Linear negation

Exponentials

References

Views

Personal tools

Navigation

Search

Tools