Translations of intuitionistic logic

Latest revision as of 21:25, 5 October 2009

The genesis of linear logic comes with a decomposition of the intuitionistic implication. Once linear logic properly defined, it corresponds to a translation of intuitionistic logic into linear logic, often called Girard's translation. In fact Jean-Yves Girard has defined two translations in his linear logic paper^[1]. We call them the call-by-name translation and the call-by-value translation.

These translations can be extended to translations of classical logic into linear logic.

[edit] Call-by-name Girard's translation 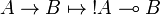$A\imp B \mapsto \oc{A}\limp B$

Formulas are translated as:

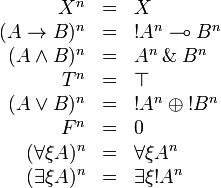
$\begin{array}{rcl} X^n & = & X \\ (A\imp B)^n & = & \oc{A^n}\limp B^n \\ (A\wedge B)^n & = & A^n \with B^n \\ T^n & = & \top \\ (A\vee B)^n & = & \oc{A^n}\plus\oc{B^n} \\ F^n & = & \zero \\ (\forall\xi A)^n & = & \forall\xi A^n \\ (\exists\xi A)^n & = & \exists\xi \oc{A^n} \end{array}$

This is extended to sequents by 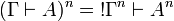$(\Gamma\vdash A)^n = \oc{\Gamma^n}\vdash A^n$ .

This allows one to translate the rules of intuitionistic logic into linear logic:

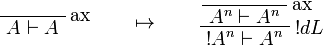
$\LabelRule{\rulename{ax}} \NulRule{A\vdash A} \DisplayProof \qquad\mapsto\qquad \LabelRule{\rulename{ax}} \NulRule{A^n\vdash A^n} \LabelRule{\oc d L} \UnaRule{\oc{A^n}\vdash A^n} \DisplayProof$

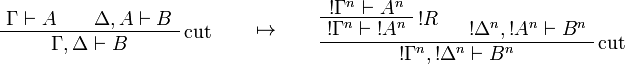
$\AxRule{\Gamma\vdash A} \AxRule{\Delta,A\vdash B} \LabelRule{\rulename{cut}} \BinRule{\Gamma,\Delta\vdash B} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash A^n} \LabelRule{\oc R} \UnaRule{\oc{\Gamma^n}\vdash \oc{A^n}} \AxRule{\oc{\Delta^n},\oc{A^n}\vdash B^n} \LabelRule{\rulename{cut}} \BinRule{\oc{\Gamma^n},\oc{\Delta^n}\vdash B^n} \DisplayProof$

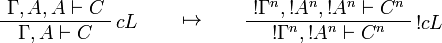
$\AxRule{\Gamma,A,A\vdash C} \LabelRule{c L} \UnaRule{\Gamma,A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n},\oc{A^n},\oc{A^n}\vdash C^n} \LabelRule{\oc c L} \UnaRule{\oc{\Gamma^n},\oc{A^n}\vdash C^n} \DisplayProof$

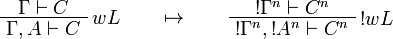
$\AxRule{\Gamma\vdash C} \LabelRule{w L} \UnaRule{\Gamma,A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash C^n} \LabelRule{\oc w L} \UnaRule{\oc{\Gamma^n},\oc{A^n}\vdash C^n} \DisplayProof$

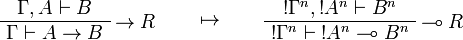
$\AxRule{\Gamma,A\vdash B} \LabelRule{\imp R} \UnaRule{\Gamma\vdash A\imp B} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n},\oc{A^n}\vdash B^n} \LabelRule{\limp R} \UnaRule{\oc{\Gamma^n}\vdash \oc{A^n}\limp B^n} \DisplayProof$

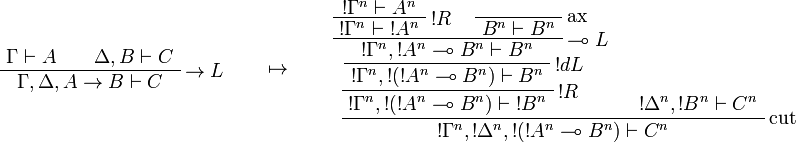
$\AxRule{\Gamma\vdash A} \AxRule{\Delta,B\vdash C} \LabelRule{\imp L} \BinRule{\Gamma,\Delta,A\imp B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash A^n} \LabelRule{\oc R} \UnaRule{\oc{\Gamma^n}\vdash \oc{A^n}} \LabelRule{\rulename{ax}} \NulRule{B^n\vdash B^n} \LabelRule{\limp L} \BinRule{\oc{\Gamma^n},\oc{A^n}\limp B^n\vdash B^n} \LabelRule{\oc d L} \UnaRule{\oc{\Gamma^n},\oc{(\oc{A^n}\limp B^n)}\vdash B^n} \LabelRule{\oc R} \UnaRule{\oc{\Gamma^n},\oc{(\oc{A^n}\limp B^n)}\vdash \oc{B^n}} \AxRule{\oc{\Delta^n},\oc{B^n}\vdash C^n} \LabelRule{\rulename{cut}} \BinRule{\oc{\Gamma^n},\oc{\Delta^n},\oc{(\oc{A^n}\limp B^n)}\vdash C^n} \DisplayProof$

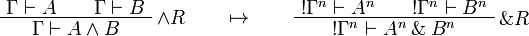
$\AxRule{\Gamma\vdash A} \AxRule{\Gamma\vdash B} \LabelRule{\wedge R} \BinRule{\Gamma\vdash A\wedge B} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash A^n} \AxRule{\oc{\Gamma^n}\vdash B^n} \LabelRule{\with R} \BinRule{\oc{\Gamma^n}\vdash A^n\with B^n} \DisplayProof$

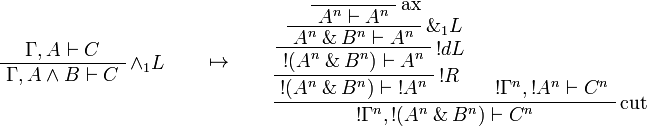
$\AxRule{\Gamma,A\vdash C} \LabelRule{\wedge_1 L} \UnaRule{\Gamma,A\wedge B\vdash C} \DisplayProof \qquad\mapsto\qquad \LabelRule{\rulename{ax}} \NulRule{A^n\vdash A^n} \LabelRule{\with_1 L} \UnaRule{A^n\with B^n\vdash A^n} \LabelRule{\oc d L} \UnaRule{\oc{(A^n\with B^n)}\vdash A^n} \LabelRule{\oc R} \UnaRule{\oc{(A^n\with B^n)}\vdash \oc{A^n}} \AxRule{\oc{\Gamma^n},\oc{A^n}\vdash C^n} \LabelRule{\rulename{cut}} \BinRule{\oc{\Gamma^n},\oc{(A^n\with B^n)}\vdash C^n} \DisplayProof$

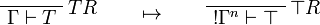
$\LabelRule{T R} \NulRule{\Gamma\vdash T} \DisplayProof \qquad\mapsto\qquad \LabelRule{\top R} \NulRule{\oc{\Gamma^n}\vdash \top} \DisplayProof$

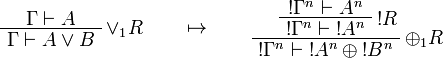
$\AxRule{\Gamma\vdash A} \LabelRule{\vee_1 R} \UnaRule{\Gamma\vdash A\vee B} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash A^n} \LabelRule{\oc R} \UnaRule{\oc{\Gamma^n}\vdash \oc{A^n}} \LabelRule{\plus_1 R} \UnaRule{\oc{\Gamma^n}\vdash \oc{A^n}\plus\oc{B^n}} \DisplayProof$

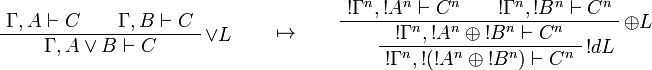
$\AxRule{\Gamma,A\vdash C} \AxRule{\Gamma,B\vdash C} \LabelRule{\vee L} \BinRule{\Gamma,A\vee B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n},\oc{A^n}\vdash C^n} \AxRule{\oc{\Gamma^n},\oc{B^n}\vdash C^n} \LabelRule{\plus L} \BinRule{\oc{\Gamma^n},\oc{A^n}\plus\oc{B^n}\vdash C^n} \LabelRule{\oc d L} \UnaRule{\oc{\Gamma^n},\oc{(\oc{A^n}\plus\oc{B^n})}\vdash C^n} \DisplayProof$

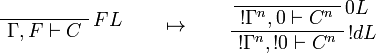
$\LabelRule{F L} \NulRule{\Gamma,F\vdash C} \DisplayProof \qquad\mapsto\qquad \LabelRule{\zero L} \NulRule{\oc{\Gamma^n},\zero\vdash C^n} \LabelRule{\oc d L} \UnaRule{\oc{\Gamma^n},\oc{\zero}\vdash C^n} \DisplayProof$

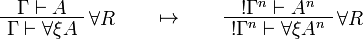
$\AxRule{\Gamma\vdash A} \LabelRule{\forall R} \UnaRule{\Gamma\vdash \forall\xi A} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash A^n} \LabelRule{\forall R} \UnaRule{\oc{\Gamma^n}\vdash \forall\xi A^n} \DisplayProof$

$\AxRule{\Gamma,A[\tau/\xi]\vdash C} \LabelRule{\forall L} \UnaRule{\Gamma,\forall\xi A\vdash C} \DisplayProof \qquad\mapsto\qquad \LabelRule{\rulename{ax}} \NulRule{A^n[\tau^n/\xi]\vdash A^n[\tau^n/\xi]} \LabelRule{\forall L} \UnaRule{\forall\xi A^n\vdash A^n[\tau^n/\xi]} \LabelRule{\oc d L} \UnaRule{\oc{\forall\xi A^n}\vdash A^n[\tau^n/\xi]} \LabelRule{\oc R} \UnaRule{\oc{\forall\xi A^n}\vdash \oc{(A^n[\tau^n/\xi])}} \AxRule{\oc{\Gamma^n},\oc{(A^n[\tau^n/\xi])}\vdash C^n} \LabelRule{\rulename{cut}} \BinRule{\oc{\Gamma^n},\oc{\forall\xi A^n}\vdash C^n} \DisplayProof$

$\AxRule{\Gamma\vdash A[\tau/\xi]} \LabelRule{\exists R} \UnaRule{\Gamma\vdash \exists\xi A} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n}\vdash A^n[\tau^n/\xi]} \LabelRule{\oc R} \UnaRule{\oc{\Gamma^n}\vdash \oc{(A^n[\tau^n/\xi])}} \LabelRule{\exists R} \UnaRule{\oc{\Gamma^n}\vdash \exists\xi\oc{A^n}} \DisplayProof$

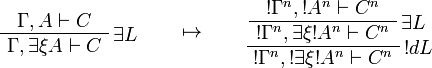
$\AxRule{\Gamma,A\vdash C} \LabelRule{\exists L} \UnaRule{\Gamma,\exists\xi A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\oc{\Gamma^n},\oc{A^n}\vdash C^n} \LabelRule{\exists L} \UnaRule{\oc{\Gamma^n},\exists\xi\oc{A^n}\vdash C^n} \LabelRule{\oc d L} \UnaRule{\oc{\Gamma^n},\oc{\exists\xi\oc{A^n}}\vdash C^n} \DisplayProof$

[edit] Call-by-value translation 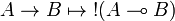$A\imp B \mapsto \oc{(A\limp B)}$

Formulas are translated as:

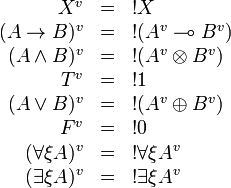
$\begin{array}{rcl} X^v & = & \oc{X} \\ (A\imp B)^v & = & \oc{(A^v\limp B^v)} \\ (A\wedge B)^v & = & \oc{(A^v \tens B^v)} \\ T^v & = & \oc{\one} \\ (A\vee B)^v & = & \oc{(A^v\plus B^v)} \\ F^v & = & \oc{\zero} \\ (\forall\xi A)^v & = & \oc{\forall\xi A^v} \\ (\exists\xi A)^v & = & \oc{\exists\xi A^v} \end{array}$

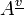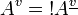The translation of any formula starts with $\oc$ , we define $A^{\underline{v}}$ such that $A^v=\oc{A^{\underline{v}}}$ .

The translation of sequents is 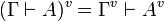$(\Gamma\vdash A)^v = \Gamma^v\vdash A^v$ .

This allows one to translate the rules of intuitionistic logic into linear logic:

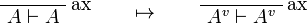
$\LabelRule{\rulename{ax}} \NulRule{A\vdash A} \DisplayProof \qquad\mapsto\qquad \LabelRule{\rulename{ax}} \NulRule{A^v\vdash A^v} \DisplayProof$

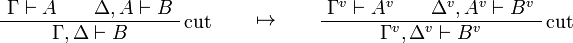
$\AxRule{\Gamma\vdash A} \AxRule{\Delta,A\vdash B} \LabelRule{\rulename{cut}} \BinRule{\Gamma,\Delta\vdash B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash A^v} \AxRule{\Delta^v,A^v\vdash B^v} \LabelRule{\rulename{cut}} \BinRule{\Gamma^v,\Delta^v\vdash B^v} \DisplayProof$

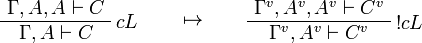
$\AxRule{\Gamma,A,A\vdash C} \LabelRule{c L} \UnaRule{\Gamma,A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v,A^v,A^v\vdash C^v} \LabelRule{\oc c L} \UnaRule{\Gamma^v,A^v\vdash C^v} \DisplayProof$

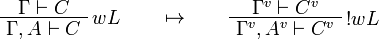
$\AxRule{\Gamma\vdash C} \LabelRule{w L} \UnaRule{\Gamma,A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash C^v} \LabelRule{\oc w L} \UnaRule{\Gamma^v,A^v\vdash C^v} \DisplayProof$

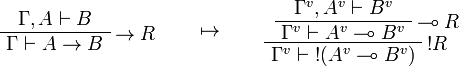
$\AxRule{\Gamma,A\vdash B} \LabelRule{\imp R} \UnaRule{\Gamma\vdash A\imp B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v,A^v\vdash B^v} \LabelRule{\limp R} \UnaRule{\Gamma^v\vdash A^v\limp B^v} \LabelRule{\oc R} \UnaRule{\Gamma^v\vdash \oc{(A^v\limp B^v)}} \DisplayProof$

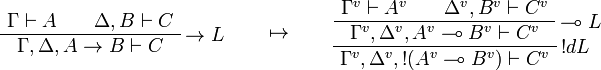
$\AxRule{\Gamma\vdash A} \AxRule{\Delta,B\vdash C} \LabelRule{\imp L} \BinRule{\Gamma,\Delta,A\imp B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash A^v} \AxRule{\Delta^v,B^v\vdash C^v} \LabelRule{\limp L} \BinRule{\Gamma^v,\Delta^v,A^v\limp B^v\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\Delta^v,\oc{(A^v\limp B^v)}\vdash C^v} \DisplayProof$

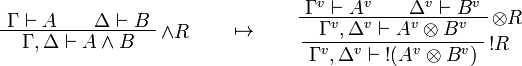
$\AxRule{\Gamma\vdash A} \AxRule{\Delta\vdash B} \LabelRule{\wedge R} \BinRule{\Gamma,\Delta\vdash A\wedge B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash A^v} \AxRule{\Delta^v\vdash B^v} \LabelRule{\tens R} \BinRule{\Gamma^v,\Delta^v\vdash A^v\tens B^v} \LabelRule{\oc R} \UnaRule{\Gamma^v,\Delta^v\vdash \oc{(A^v\tens B^v)}} \DisplayProof$

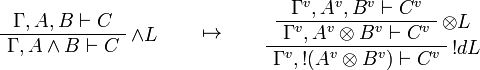
$\AxRule{\Gamma,A,B\vdash C} \LabelRule{\wedge L} \UnaRule{\Gamma,A\wedge B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v,A^v,B^v\vdash C^v} \LabelRule{\tens L} \UnaRule{\Gamma^v,A^v\tens B^v\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\oc{(A^v\tens B^v)}\vdash C^v} \DisplayProof$

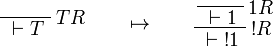
$\LabelRule{T R} \NulRule{{}\vdash T} \DisplayProof \qquad\mapsto\qquad \LabelRule{\one R} \NulRule{{}\vdash \one} \LabelRule{\oc R} \UnaRule{{}\vdash \oc{\one}} \DisplayProof$

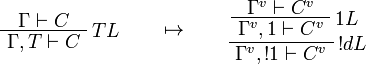
$\AxRule{\Gamma\vdash C} \LabelRule{T L} \UnaRule{\Gamma,T\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash C^v} \LabelRule{\one L} \UnaRule{\Gamma^v,\one\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\oc{\one}\vdash C^v} \DisplayProof$

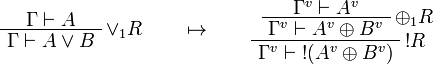
$\AxRule{\Gamma\vdash A} \LabelRule{\vee_1 R} \UnaRule{\Gamma\vdash A\vee B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash A^v} \LabelRule{\plus_1 R} \UnaRule{\Gamma^v\vdash A^v\plus B^v} \LabelRule{\oc R} \UnaRule{\Gamma^v\vdash \oc{(A^v\plus B^v)}} \DisplayProof$

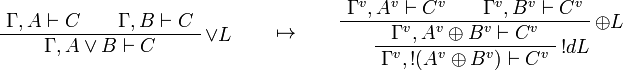
$\AxRule{\Gamma,A\vdash C} \AxRule{\Gamma,B\vdash C} \LabelRule{\vee L} \BinRule{\Gamma,A\vee B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v,A^v\vdash C^v} \AxRule{\Gamma^v,B^v\vdash C^v} \LabelRule{\plus L} \BinRule{\Gamma^v,A^v\plus B^v\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\oc{(A^v\plus B^v)}\vdash C^v} \DisplayProof$

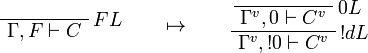
$\LabelRule{F L} \NulRule{\Gamma,F\vdash C} \DisplayProof \qquad\mapsto\qquad \LabelRule{\zero L} \NulRule{\Gamma^v,\zero\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\oc{\zero}\vdash C^v} \DisplayProof$

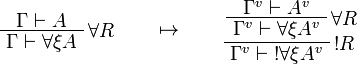
$\AxRule{\Gamma\vdash A} \LabelRule{\forall R} \UnaRule{\Gamma\vdash \forall\xi A} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash A^v} \LabelRule{\forall R} \UnaRule{\Gamma^v\vdash \forall\xi A^v} \LabelRule{\oc R} \UnaRule{\Gamma^v\vdash \oc{\forall\xi A^v}} \DisplayProof$

We use $(A[\tau/\xi])^v=A^v[\tau^{\underline{v}}/\xi]$ .

$\AxRule{\Gamma,A[\tau/\xi]\vdash C} \LabelRule{\forall L} \UnaRule{\Gamma,\forall\xi A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v,A^v[\tau^{\underline{v}}/\xi]\vdash C^v} \LabelRule{\forall L} \UnaRule{\Gamma^v,\forall\xi A^v\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\oc{\forall\xi A^v}\vdash C^v} \DisplayProof$

$\AxRule{\Gamma\vdash A[\tau/\xi]} \LabelRule{\exists R} \UnaRule{\Gamma\vdash \exists\xi A} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v\vdash A^v[\tau^{\underline{v}}/\xi]} \LabelRule{\exists R} \UnaRule{\Gamma^v\vdash \exists\xi A^v} \LabelRule{\oc R} \UnaRule{\Gamma^v\vdash \oc{\exists\xi A^v}} \DisplayProof$

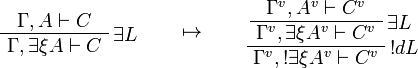
$\AxRule{\Gamma,A\vdash C} \LabelRule{\exists L} \UnaRule{\Gamma,\exists\xi A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^v,A^v\vdash C^v} \LabelRule{\exists L} \UnaRule{\Gamma^v,\exists\xi A^v\vdash C^v} \LabelRule{\oc d L} \UnaRule{\Gamma^v,\oc{\exists\xi A^v}\vdash C^v} \DisplayProof$

[edit] Alternative presentation

It is also possible to define 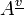$A^{\underline{v}}$ as the primitive construction.

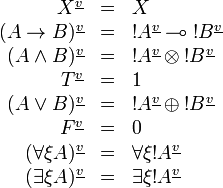
$\begin{array}{rcl} X^{\underline{v}} & = & X \\ (A\imp B)^{\underline{v}} & = & \oc{A^{\underline{v}}}\limp\oc{B^{\underline{v}}} \\ (A\wedge B)^{\underline{v}} & = & \oc{A^{\underline{v}}}\tens\oc{B^{\underline{v}}} \\ T^{\underline{v}} & = & \one \\ (A\vee B)^{\underline{v}} & = & \oc{A^{\underline{v}}}\plus\oc{B^{\underline{v}}} \\ F^{\underline{v}} & = & \zero \\ (\forall\xi A)^{\underline{v}} & = & \forall\xi \oc{A^{\underline{v}}} \\ (\exists\xi A)^{\underline{v}} & = & \exists\xi \oc{A^{\underline{v}}} \end{array}$

If we define 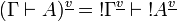$(\Gamma\vdash A)^{\underline{v}} = \oc{\Gamma^{\underline{v}}}\vdash\oc{A^{\underline{v}}}$ , we have 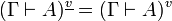$(\Gamma\vdash A)^{\underline{v}} = (\Gamma\vdash A)^v$ and thus we obtain the same translation of proofs.

[edit] Call-by-value Girard's translation 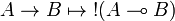$A\imp B \mapsto \oc{(A\limp B)}$

The original version of the call-by-value translation given by Jean-Yves Girard^[1] is an optimisation of the previous one using properties of positive formulas.

Formulas are translated as:

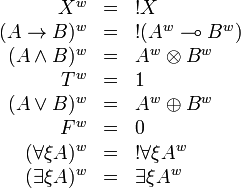
$\begin{array}{rcl} X^w & = & \oc{X} \\ (A\imp B)^w & = & \oc{(A^w\limp B^w)} \\ (A\wedge B)^w & = & A^w \tens B^w \\ T^w & = & \one \\ (A\vee B)^w & = & A^w\plus B^w \\ F^w & = & \zero \\ (\forall\xi A)^w & = & \oc{\forall\xi A^w} \\ (\exists\xi A)^w & = & \exists\xi A^w \end{array}$

The translation of any formula is a positive formula.

The translation of sequents is 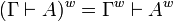$(\Gamma\vdash A)^w = \Gamma^w\vdash A^w$ .

This allows one to translate the rules of intuitionistic logic into linear logic:

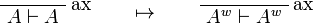
$\LabelRule{\rulename{ax}} \NulRule{A\vdash A} \DisplayProof \qquad\mapsto\qquad \LabelRule{\rulename{ax}} \NulRule{A^w\vdash A^w} \DisplayProof$

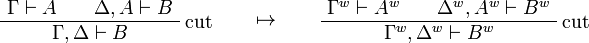
$\AxRule{\Gamma\vdash A} \AxRule{\Delta,A\vdash B} \LabelRule{\rulename{cut}} \BinRule{\Gamma,\Delta\vdash B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash A^w} \AxRule{\Delta^w,A^w\vdash B^w} \LabelRule{\rulename{cut}} \BinRule{\Gamma^w,\Delta^w\vdash B^w} \DisplayProof$

$\AxRule{\Gamma,A,A\vdash C} \LabelRule{c L} \UnaRule{\Gamma,A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w,A^w,A^w\vdash C^w} \LabelRule{+ c L} \UnaRule{\Gamma^w,A^w\vdash C^w} \DisplayProof$

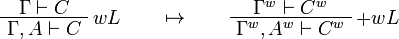
$\AxRule{\Gamma\vdash C} \LabelRule{w L} \UnaRule{\Gamma,A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash C^w} \LabelRule{+ w L} \UnaRule{\Gamma^w,A^w\vdash C^w} \DisplayProof$

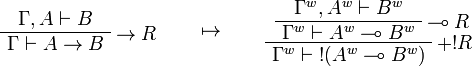
$\AxRule{\Gamma,A\vdash B} \LabelRule{\imp R} \UnaRule{\Gamma\vdash A\imp B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w,A^w\vdash B^w} \LabelRule{\limp R} \UnaRule{\Gamma^w\vdash A^w\limp B^w} \LabelRule{+ \oc R} \UnaRule{\Gamma^w\vdash \oc{(A^w\limp B^w)}} \DisplayProof$

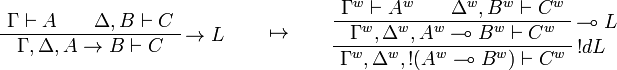
$\AxRule{\Gamma\vdash A} \AxRule{\Delta,B\vdash C} \LabelRule{\imp L} \BinRule{\Gamma,\Delta,A\imp B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash A^w} \AxRule{\Delta^w,B^w\vdash C^w} \LabelRule{\limp L} \BinRule{\Gamma^w,\Delta^w,A^w\limp B^w\vdash C^w} \LabelRule{\oc d L} \UnaRule{\Gamma^w,\Delta^w,\oc{(A^w\limp B^w)}\vdash C^w} \DisplayProof$

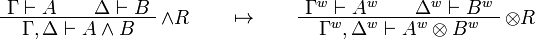
$\AxRule{\Gamma\vdash A} \AxRule{\Delta\vdash B} \LabelRule{\wedge R} \BinRule{\Gamma,\Delta\vdash A\wedge B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash A^w} \AxRule{\Delta^w\vdash B^w} \LabelRule{\tens R} \BinRule{\Gamma^w,\Delta^w\vdash A^w\tens B^w} \DisplayProof$

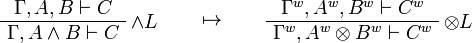
$\AxRule{\Gamma,A,B\vdash C} \LabelRule{\wedge L} \UnaRule{\Gamma,A\wedge B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w,A^w,B^w\vdash C^w} \LabelRule{\tens L} \UnaRule{\Gamma^w,A^w\tens B^w\vdash C^w} \DisplayProof$

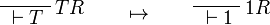
$\LabelRule{T R} \NulRule{{}\vdash T} \DisplayProof \qquad\mapsto\qquad \LabelRule{\one R} \NulRule{{}\vdash \one} \DisplayProof$

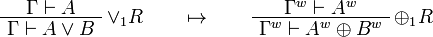
$\AxRule{\Gamma\vdash A} \LabelRule{\vee_1 R} \UnaRule{\Gamma\vdash A\vee B} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash A^w} \LabelRule{\plus_1 R} \UnaRule{\Gamma^w\vdash A^w\plus B^w} \DisplayProof$

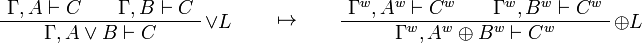
$\AxRule{\Gamma,A\vdash C} \AxRule{\Gamma,B\vdash C} \LabelRule{\vee L} \BinRule{\Gamma,A\vee B\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w,A^w\vdash C^w} \AxRule{\Gamma^w,B^w\vdash C^w} \LabelRule{\plus L} \BinRule{\Gamma^w,A^w\plus B^w\vdash C^w} \DisplayProof$

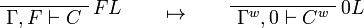
$\LabelRule{F L} \NulRule{\Gamma,F\vdash C} \DisplayProof \qquad\mapsto\qquad \LabelRule{\zero L} \NulRule{\Gamma^w,\zero\vdash C^w} \DisplayProof$

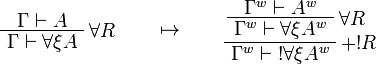
$\AxRule{\Gamma\vdash A} \LabelRule{\forall R} \UnaRule{\Gamma\vdash \forall\xi A} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash A^w} \LabelRule{\forall R} \UnaRule{\Gamma^w\vdash \forall\xi A^w} \LabelRule{+ \oc R} \UnaRule{\Gamma^w\vdash \oc{\forall\xi A^w}} \DisplayProof$

We use $(A[\tau/\xi])^w\linequiv A^w[\tau^w/\xi]$ .

$\AxRule{\Gamma,A[\tau/\xi]\vdash C} \LabelRule{\forall L} \UnaRule{\Gamma,\forall\xi A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w,(A[\tau/\xi])^w\vdash C^w} \UnaRule{\Gamma^w,A^w[\tau^w/\xi]\vdash C^w} \LabelRule{\forall L} \UnaRule{\Gamma^w,\forall\xi A^w\vdash C^w} \LabelRule{\oc d L} \UnaRule{\Gamma^w,\oc{\forall\xi A^w}\vdash C^w} \DisplayProof$

$\AxRule{\Gamma\vdash A[\tau/\xi]} \LabelRule{\exists R} \UnaRule{\Gamma\vdash \exists\xi A} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w\vdash (A[\tau/\xi])^w} \UnaRule{\Gamma^w\vdash A^w[\tau^w/\xi]} \LabelRule{\exists R} \UnaRule{\Gamma^w\vdash \exists\xi A^w} \DisplayProof$

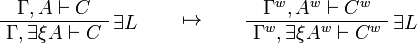
$\AxRule{\Gamma,A\vdash C} \LabelRule{\exists L} \UnaRule{\Gamma,\exists\xi A\vdash C} \DisplayProof \qquad\mapsto\qquad \AxRule{\Gamma^w,A^w\vdash C^w} \LabelRule{\exists L} \UnaRule{\Gamma^w,\exists\xi A^w\vdash C^w} \DisplayProof$

[edit] References

↑ ^1.0 ^1.1 Girard, Jean-Yves. Linear logic. Theoretical Computer Science. Volume 50, Issue 1, pp. 1-101, doi:10.1016/0304-3975(87)90045-4, 1987.

[ll-0] 1.0 ^1.1 Girard, Jean-Yves. Linear logic. Theoretical Computer Science. Volume 50, Issue 1, pp. 1-101, doi:10.1016/0304-3975(87)90045-4, 1987.

[1]

Translations of intuitionistic logic

Latest revision as of 21:25, 5 October 2009

Contents

[edit] Call-by-name Girard's translation $A\imp B \mapsto \oc{A}\limp B$

[edit] Call-by-value translation $A\imp B \mapsto \oc{(A\limp B)}$

[edit] Alternative presentation

[edit] Call-by-value Girard's translation $A\imp B \mapsto \oc{(A\limp B)}$

[edit] References

Views

Personal tools

Navigation

Search

Tools

@@ Line 31: / Line 31: @@
 \LabelRule{\rulename{ax}}
 \NulRule{A^n\vdash A^n}
-\LabelRule{\oc L}
+\LabelRule{\oc d L}
 \UnaRule{\oc{A^n}\vdash A^n}
 \DisplayProof
@@ Line 300: / Line 300: @@
 (A\vee B)^v & = & \oc{(A^v\plus B^v)} \\
 F^v & = & \oc{\zero} \\
-(\forall\xi A)^v & = & \oc{(\forall\xi A^v)} \\
+(\forall\xi A)^v & = & \oc{\forall\xi A^v} \\
-(\exists\xi A)^v & = & \oc{(\exists\xi A^v)}
+(\exists\xi A)^v & = & \oc{\exists\xi A^v}
 \end{array}
 </math>
@@ Line 312: / Line 312: @@
 <math>
-\LabelRule{\textit{ax}}
+\LabelRule{\rulename{ax}}
 \NulRule{A\vdash A}
 \DisplayProof
 \qquad\mapsto\qquad
-\LabelRule{\textit{ax}}
+\LabelRule{\rulename{ax}}
 \NulRule{A^v\vdash A^v}
 \DisplayProof
@@ Line 326: / Line 326: @@
 \AxRule{\Gamma\vdash A}
 \AxRule{\Delta,A\vdash B}
-\LabelRule{\textit{cut}}
+\LabelRule{\rulename{cut}}
 \BinRule{\Gamma,\Delta\vdash B}
 \DisplayProof
@@ Line 332: / Line 332: @@
 \AxRule{\Gamma^v\vdash A^v}
 \AxRule{\Delta^v,A^v\vdash B^v}
-\LabelRule{\textit{cut}}
+\LabelRule{\rulename{cut}}
 \BinRule{\Gamma^v,\Delta^v\vdash B^v}
 \DisplayProof
@@ Line 394: / Line 394: @@
 \LabelRule{\limp L}
 \BinRule{\Gamma^v,\Delta^v,A^v\limp B^v\vdash C^v}
-\LabelRule{\oc L}
+\LabelRule{\oc d L}
 \UnaRule{\Gamma^v,\Delta^v,\oc{(A^v\limp B^v)}\vdash C^v}
 \DisplayProof
@@ Line 428: / Line 428: @@
 \LabelRule{\tens L}
 \UnaRule{\Gamma^v,A^v\tens B^v\vdash C^v}
-\LabelRule{\oc L}
+\LabelRule{\oc d L}
 \UnaRule{\Gamma^v,\oc{(A^v\tens B^v)}\vdash C^v}
 \DisplayProof
@@ Line 444: / Line 444: @@
 \LabelRule{\oc R}
 \UnaRule{{}\vdash \oc{\one}}
+\DisplayProof
+</math>
+<br />
+<math>
+\AxRule{\Gamma\vdash C}
+\LabelRule{T L}
+\UnaRule{\Gamma,T\vdash C}
+\DisplayProof
+\qquad\mapsto\qquad
+\AxRule{\Gamma^v\vdash C^v}
+\LabelRule{\one L}
+\UnaRule{\Gamma^v,\one\vdash C^v}
+\LabelRule{\oc d L}
+\UnaRule{\Gamma^v,\oc{\one}\vdash C^v}
 \DisplayProof
 </math>
@@ Line 524: / Line 540: @@
 \LabelRule{\forall L}
 \UnaRule{\Gamma^v,\forall\xi A^v\vdash C^v}
-\LabelRule{\oc L}
+\LabelRule{\oc d L}
-\UnaRule{\Gamma^v,\oc{(\forall\xi A^v)}\vdash C^v}
+\UnaRule{\Gamma^v,\oc{\forall\xi A^v}\vdash C^v}
 \DisplayProof
 </math>
@@ Line 580: / Line 596: @@
 If we define <math>(\Gamma\vdash A)^{\underline{v}} = \oc{\Gamma^{\underline{v}}}\vdash\oc{A^{\underline{v}}}</math>, we have <math>(\Gamma\vdash A)^{\underline{v}} = (\Gamma\vdash A)^v</math> and thus we obtain the same translation of proofs.
 == Call-by-value Girard's translation <math>A\imp B \mapsto \oc{(A\limp B)}</math> ==
@@ Line 596: / Line 611: @@
 (A\vee B)^w & = & A^w\plus B^w \\
 F^w & = & \zero \\
-(\forall\xi A)^w & = & \oc{(\forall\xi A^w)} \\
+(\forall\xi A)^w & = & \oc{\forall\xi A^w} \\
 (\exists\xi A)^w & = & \exists\xi A^w
 \end{array}
@@ Line 608: / Line 623: @@
 <math>
-\LabelRule{\textit{ax}}
+\LabelRule{\rulename{ax}}
 \NulRule{A\vdash A}
 \DisplayProof
 \qquad\mapsto\qquad
-\LabelRule{\textit{ax}}
+\LabelRule{\rulename{ax}}
 \NulRule{A^w\vdash A^w}
 \DisplayProof
@@ Line 622: / Line 637: @@
 \AxRule{\Gamma\vdash A}
 \AxRule{\Delta,A\vdash B}
-\LabelRule{\textit{cut}}
+\LabelRule{\rulename{cut}}
 \BinRule{\Gamma,\Delta\vdash B}
 \DisplayProof
@@ Line 628: / Line 643: @@
 \AxRule{\Gamma^w\vdash A^w}
 \AxRule{\Delta^w,A^w\vdash B^w}
-\LabelRule{\textit{cut}}
+\LabelRule{\rulename{cut}}
 \BinRule{\Gamma^w,\Delta^w\vdash B^w}
 \DisplayProof
@@ Line 672: / Line 687: @@
 \LabelRule{\limp R}
 \UnaRule{\Gamma^w\vdash A^w\limp B^w}
-\LabelRule{\oc R}
+\LabelRule{+ \oc R}
 \UnaRule{\Gamma^w\vdash \oc{(A^w\limp B^w)}}
 \DisplayProof
@@ Line 690: / Line 705: @@
 \LabelRule{\limp L}
 \BinRule{\Gamma^w,\Delta^w,A^w\limp B^w\vdash C^w}
-\LabelRule{\oc L}
+\LabelRule{\oc d L}
 \UnaRule{\Gamma^w,\Delta^w,\oc{(A^w\limp B^w)}\vdash C^w}
 \DisplayProof
@@ Line 790: / Line 805: @@
 \LabelRule{\forall R}
 \UnaRule{\Gamma^w\vdash \forall\xi A^w}
-\LabelRule{\oc R}
+\LabelRule{+ \oc R}
 \UnaRule{\Gamma^w\vdash \oc{\forall\xi A^w}}
 \DisplayProof
@@ Line 809: / Line 824: @@
 \LabelRule{\forall L}
 \UnaRule{\Gamma^w,\forall\xi A^w\vdash C^w}
-\LabelRule{\oc L}
+\LabelRule{\oc d L}
-\UnaRule{\Gamma^w,\oc{(\forall\xi A^w)}\vdash C^w}
+\UnaRule{\Gamma^w,\oc{\forall\xi A^w}\vdash C^w}
 \DisplayProof
 </math>
@@ Line 842: / Line 857: @@
 \DisplayProof
 </math>
 == References ==