Intuitionistic linear logic

Latest revision as of 09:31, 13 March 2017

Intuitionistic Linear Logic ( $I L L$ ) is the intuitionnistic restriction of linear logic: the sequent calculus of $I L L$ is obtained from the two-sided sequent calculus of linear logic by constraining sequents to have exactly one formula on the right-hand side: 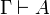$\Gamma\vdash A$ .

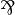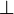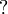The connectives $\parr$ , $\bot$ and $\wn$ are not available anymore, but the linear implication 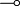$\limp$ is.

[edit] Sequent Calculus

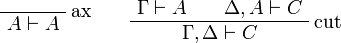
$\LabelRule{\rulename{ax}} \NulRule{A\vdash A} \DisplayProof \qquad \AxRule{\Gamma\vdash A} \AxRule{\Delta,A\vdash C} \LabelRule{\rulename{cut}} \BinRule{\Gamma,\Delta\vdash C} \DisplayProof$

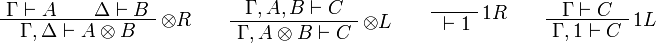
$\AxRule{\Gamma\vdash A} \AxRule{\Delta\vdash B} \LabelRule{\tens R} \BinRule{\Gamma,\Delta\vdash A\tens B} \DisplayProof \qquad \AxRule{\Gamma,A,B\vdash C} \LabelRule{\tens L} \UnaRule{\Gamma,A\tens B\vdash C} \DisplayProof \qquad \LabelRule{\one R} \NulRule{{}\vdash\one} \DisplayProof \qquad \AxRule{\Gamma\vdash C} \LabelRule{\one L} \UnaRule{\Gamma,\one\vdash C} \DisplayProof$

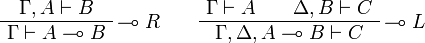
$\AxRule{\Gamma,A\vdash B} \LabelRule{\limp R} \UnaRule{\Gamma\vdash A\limp B} \DisplayProof \qquad \AxRule{\Gamma\vdash A} \AxRule{\Delta,B\vdash C} \LabelRule{\limp L} \BinRule{\Gamma,\Delta,A\limp B\vdash C} \DisplayProof$

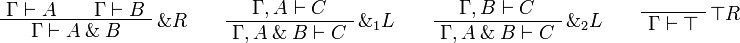
$\AxRule{\Gamma\vdash A} \AxRule{\Gamma\vdash B} \LabelRule{\with R} \BinRule{\Gamma\vdash A\with B} \DisplayProof \qquad \AxRule{\Gamma,A\vdash C} \LabelRule{\with_1 L} \UnaRule{\Gamma,A\with B\vdash C} \DisplayProof \qquad \AxRule{\Gamma,B\vdash C} \LabelRule{\with_2 L} \UnaRule{\Gamma,A\with B\vdash C} \DisplayProof \qquad \LabelRule{\top R} \NulRule{\Gamma\vdash\top} \DisplayProof$

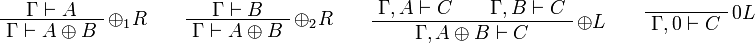
$\AxRule{\Gamma\vdash A} \LabelRule{\plus_1 R} \UnaRule{\Gamma\vdash A\plus B} \DisplayProof \qquad \AxRule{\Gamma\vdash B} \LabelRule{\plus_2 R} \UnaRule{\Gamma\vdash A\plus B} \DisplayProof \qquad \AxRule{\Gamma,A\vdash C} \AxRule{\Gamma,B\vdash C} \LabelRule{\plus L} \BinRule{\Gamma,A\plus B\vdash C} \DisplayProof \qquad \LabelRule{\zero L} \NulRule{\Gamma,\zero\vdash C} \DisplayProof$

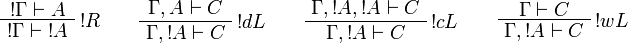
$\AxRule{\oc{\Gamma}\vdash A} \LabelRule{\oc R} \UnaRule{\oc{\Gamma}\vdash\oc{A}} \DisplayProof \qquad \AxRule{\Gamma,A\vdash C} \LabelRule{\oc d L} \UnaRule{\Gamma,\oc{A}\vdash C} \DisplayProof \qquad \AxRule{\Gamma,\oc{A},\oc{A}\vdash C} \LabelRule{\oc c L} \UnaRule{\Gamma,\oc{A}\vdash C} \DisplayProof \qquad \AxRule{\Gamma\vdash C} \LabelRule{\oc w L} \UnaRule{\Gamma,\oc{A}\vdash C} \DisplayProof$

$\AxRule{\Gamma\vdash A} \LabelRule{\forall R} \UnaRule{\Gamma\vdash \forall\xi A} \DisplayProof \qquad \AxRule{\Gamma,A[\tau/\xi]\vdash C} \LabelRule{\forall L} \UnaRule{\Gamma,\forall\xi A\vdash C} \DisplayProof \qquad \AxRule{\Gamma\vdash A[\tau/\xi]} \LabelRule{\exists R} \UnaRule{\Gamma\vdash\exists\xi A} \DisplayProof \qquad \AxRule{\Gamma,A\vdash C} \LabelRule{\exists L} \UnaRule{\Gamma,\exists\xi A\vdash C} \DisplayProof$

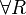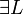with $ξ$ not free in $Γ, C$ in the rules $\forall R$ and $\exists L$ .

[edit] The intuitionistic fragment of linear logic

In order to characterize intuitionistic linear logic inside linear logic, we define the intuitionistic restriction of linear formulas:

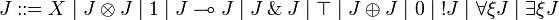
$J ::= X \mid J\tens J \mid \one \mid J\limp J \mid J\with J \mid \top \mid J\plus J \mid \zero \mid \oc{J} \mid \forall\xi J \mid \exists\xi J$

$J L L$ is the fragment of linear logic obtained by restriction to intuitionistic formulas.

Proposition (From $I L L$ to $J L L$ )

If 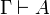$\Gamma\vdash A$ is provable in $I L L 012$ , it is provable in $J L L 012$ .

Proof. $I L L 012$ is included in $J L L 012$ .

Theorem (From $J L L$ to $I L L$ )

If 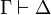$\Gamma\vdash\Delta$ is provable in $J L L 12$ , it is provable in $I L L 12$ .

Proof. We only prove the first order case, a proof of the full result is given in the PhD thesis of Harold Schellinx^[1].

Consider a cut-free proof of 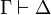$\Gamma\vdash\Delta$ in $J L L 12$ , we can prove by induction on the length of such a proof that it belongs to $I L L 12$ .

Corollary (Unique conclusion in $J L L$ )

If 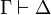$\Gamma\vdash\Delta$ is provable in $J L L 12$ then $Δ$ is a singleton.

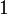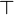The theorem is also valid for formulas containing $\one$ or $\top$ but not anymore with 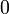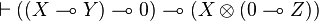$\zero$ . ${}\vdash((X\limp Y)\limp\zero)\limp(X\tens(\zero\limp Z))$ is provable in $J L L 0$ :

$\LabelRule{\rulename{ax}} \NulRule{X\vdash X} \LabelRule{\zero L} \NulRule{\zero\vdash Y,Z} \LabelRule{\limp R} \UnaRule{{}\vdash Y,\zero\limp Z} \LabelRule{\tens R} \BinRule{X\vdash Y,X\tens(\zero\limp Z)} \LabelRule{\limp R} \UnaRule{{}\vdash X\limp Y,X\tens(\zero\limp Z)} \LabelRule{\zero L} \NulRule{\zero\vdash {}} \LabelRule{\limp L} \BinRule{(X\limp Y)\limp\zero\vdash X\tens(\zero\limp Z)} \LabelRule{\limp R} \UnaRule{{}\vdash((X\limp Y)\limp\zero)\limp(X\tens(\zero\limp Z))} \DisplayProof$

but not in $I L L 0$ .

[edit] Input / output polarities

In order to go to $L L$ without $\limp$ , we consider two classes of formulas: input formulas ( $I$ ) and output formulas ( $O$ ).

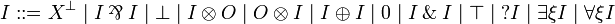
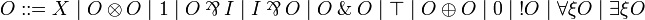
$I ::= X\orth \mid I\parr I \mid \bot \mid I\tens O \mid O\tens I \mid I\plus I \mid \zero \mid I\with I \mid \top \mid \wn{I} \mid \exists\xi I \mid \forall\xi I$ $O ::= X \mid O\tens O \mid \one \mid O\parr I \mid I\parr O \mid O\with O \mid \top \mid O\plus O \mid \zero \mid \oc{O} \mid \forall\xi O \mid \exists\xi O$

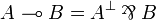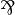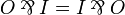By applying the definition of the linear implication $A\limp B = A\orth\parr B$ , any formula of $J L L$ is mapped to an output formula (and the dual of a $J L L$ formula to an input formula). Conversely, any output formula is coming from a $J L L$ formula in this way (up to commutativity of $\parr$ : $O\parr I = I\parr O$ ).

The fragment of linear logic obtained by restriction to input/output formulas is thus equivalent to $J L L$ , but the closure of the set of input/output formulas under orthogonal allows for a one-sided presentation.

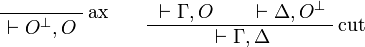
$\LabelRule{\rulename{ax}} \NulRule{\vdash O\orth,O} \DisplayProof \qquad \AxRule{{}\vdash \Gamma,O} \AxRule{{}\vdash\Delta,O\orth} \LabelRule{\rulename{cut}} \BinRule{{}\vdash\Gamma,\Delta} \DisplayProof$

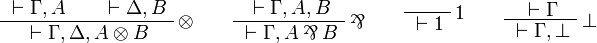
$\AxRule{{}\vdash\Gamma,A} \AxRule{{}\vdash\Delta,B} \LabelRule{\tens} \BinRule{{}\vdash\Gamma,\Delta,A\tens B} \DisplayProof \qquad \AxRule{{}\vdash\Gamma,A,B} \LabelRule{\parr} \UnaRule{{}\vdash\Gamma,A\parr B} \DisplayProof \qquad \LabelRule{\one} \NulRule{{}\vdash\one} \DisplayProof \qquad \AxRule{{}\vdash\Gamma} \LabelRule{\bot} \UnaRule{{}\vdash\Gamma,\bot} \DisplayProof$

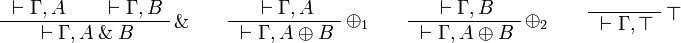
$\AxRule{{}\vdash\Gamma,A} \AxRule{{}\vdash\Gamma,B} \LabelRule{\with} \BinRule{{}\vdash\Gamma,A\with B} \DisplayProof \qquad \AxRule{{}\vdash\Gamma,A} \LabelRule{\plus_1} \UnaRule{{}\vdash\Gamma,A\plus B} \DisplayProof \qquad \AxRule{{}\vdash\Gamma,B} \LabelRule{\plus_2} \UnaRule{{}\vdash\Gamma,A\plus B} \DisplayProof \qquad \LabelRule{\top} \NulRule{{}\vdash\Gamma,\top} \DisplayProof$

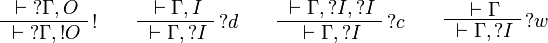
$\AxRule{{}\vdash\wn{\Gamma},O} \LabelRule{\oc} \UnaRule{{}\vdash\wn{\Gamma},\oc{O}} \DisplayProof \qquad \AxRule{{}\vdash\Gamma,I} \LabelRule{\wn d} \UnaRule{{}\vdash\Gamma,\wn{I}} \DisplayProof \qquad \AxRule{{}\vdash\Gamma,\wn{I},\wn{I}} \LabelRule{\wn c} \UnaRule{{}\vdash\Gamma,\wn{I}} \DisplayProof \qquad \AxRule{{}\vdash\Gamma} \LabelRule{\wn w} \UnaRule{{}\vdash\Gamma,\wn{I}} \DisplayProof$

$\AxRule{{}\vdash\Gamma,A} \LabelRule{\forall} \UnaRule{{}\vdash\Gamma,\forall\xi A} \DisplayProof \qquad \AxRule{{}\vdash\Gamma,A[\tau/\xi]} \LabelRule{\exists} \UnaRule{{}\vdash\Gamma,\exists\xi A} \DisplayProof$

with $A$ and $B$ arbitrary input or output formulas (under the condition that the composite formulas containing them are input or output formulas) and $ξ$ not free in $Γ$ in the rule 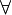$\forall$ .

Lemma (Output formula)

If 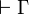${}\vdash\Gamma$ is provable in $L L 12$ and contains only input and output formulas, then $Γ$ contains exactly one output formula.

Proof. Assume $Γ O$ is obtained by turning the output formulas of $Γ$ into $J L L$ formulas and $Γ I$ is obtained by turning the dual of the input formulas of $Γ$ into $J L L$ formulas, 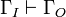$\Gamma_I\vdash\Gamma_O$ is provable in $L L 12$ thus in $J L L 12$ . By corollary (Unique conclusion in $J L L$ ), $Γ O$ is a singleton, thus $Γ$ contains exactly one output formula.

[edit] References

↑ Schellinx, Harold. The Noble Art of Linear Decorating. Dissertation series of the Dutch Institute for Logic, Language and Computation. University of Amsterdam. ILLC-Dissertation Series, 1994-1, 1994.

[0] Schellinx, Harold. The Noble Art of Linear Decorating. Dissertation series of the Dutch Institute for Logic, Language and Computation. University of Amsterdam. ILLC-Dissertation Series, 1994-1, 1994.

[1]

Intuitionistic linear logic

Latest revision as of 09:31, 13 March 2017

Contents

[edit] Sequent Calculus

[edit] The intuitionistic fragment of linear logic

[edit] Input / output polarities

[edit] References

Views

Personal tools

Navigation

Search

Tools

@@ Line 1: / Line 1: @@
 Intuitionistic Linear Logic (<math>ILL</math>) is the
 [[intuitionnistic restriction]] of linear logic: the sequent calculus
-of <math>ILL</math> is obtained from the two-sided sequent calculus of
+of <math>ILL</math> is obtained from the [[Sequent calculus#Sequents and proofs|two-sided sequent calculus of
-linear logic by constraining sequents to have exactly one formula on
+linear logic]] by constraining sequents to have exactly one formula on
 the right-hand side: <math>\Gamma\vdash A</math>.
@@ Line 191: / Line 191: @@
 }}
-The theorem is still valid with for formulas containing <math>\one</math> but not anymore with <math>\top</math> and <math>\zero</math>. <math>{}\vdash((X\limp Y)\limp\zero)\limp(X\tens\top)</math> is provable in <math>JLL_0</math>:
+The theorem is also valid for formulas containing <math>\one</math> or <math>\top</math> but not anymore with <math>\zero</math>. <math>{}\vdash((X\limp Y)\limp\zero)\limp(X\tens(\zero\limp Z))</math> is provable in <math>JLL_0</math>:
 <math>
 \LabelRule{\rulename{ax}}
 \NulRule{X\vdash X}
-\LabelRule{\top R}
+\LabelRule{\zero L}
-\NulRule{{}\vdash Y,\top}
+\NulRule{\zero\vdash Y,Z}
+\LabelRule{\limp R}
+\UnaRule{{}\vdash Y,\zero\limp Z}
 \LabelRule{\tens R}
-\BinRule{X\vdash Y,X\tens\top}
+\BinRule{X\vdash Y,X\tens(\zero\limp Z)}
 \LabelRule{\limp R}
-\UnaRule{{}\vdash X\limp Y,X\tens\top}
+\UnaRule{{}\vdash X\limp Y,X\tens(\zero\limp Z)}
 \LabelRule{\zero L}
 \NulRule{\zero\vdash {}}
 \LabelRule{\limp L}
-\BinRule{(X\limp Y)\limp\zero\vdash X\tens\top}
+\BinRule{(X\limp Y)\limp\zero\vdash X\tens(\zero\limp Z)}
 \LabelRule{\limp R}
-\UnaRule{{}\vdash((X\limp Y)\limp\zero)\limp(X\tens\top)}
+\UnaRule{{}\vdash((X\limp Y)\limp\zero)\limp(X\tens(\zero\limp Z))}
 \DisplayProof
 </math>