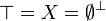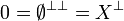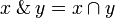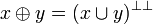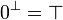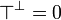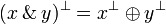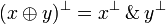Phase semantics
(initial page: preliminaries and additives) |
Remi Nollet (Talk | contribs) m (“absorbant” ~> “absorbing”) |
||
| (25 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | =Introduction= |
+ | ==Introduction== |
| − | The semantics given by phase spaces is a kind of "truth semantics", and is thus quite different from the more usual denotational semantics of linear logic. (Those are rather some "proof semantics".) |
+ | The semantics given by phase spaces is a kind of "formula and provability semantics", and is thus quite different in spirit from the more usual denotational semantics of linear logic. (Those are rather some "formulas and ''proofs'' semantics".) |
--- probably a whole lot more of blabla to put here... --- |
--- probably a whole lot more of blabla to put here... --- |
||
| + | ==Preliminaries: relation and closure operators== |
||
| + | Part of the structure obtained from phase semantics works in a very general framework and relies solely on the notion of relation between two sets. |
||
| − | =Preliminaries: relation and closure operators= |
||
| − | + | ===Relations and operators on subsets=== |
|
| − | ==Relations and operators on subsets== |
||
The starting point of phase semantics is the notion of ''duality''. The structure needed to talk about duality is very simple: one just needs a relation <math>R</math> between two sets <math>X</math> and <math>Y</math>. Using standard mathematical practice, we can write either <math>(a,b) \in R</math> or <math>a\mathrel{R} b</math> to say that <math>a\in X</math> and <math>b\in Y</math> are related. |
The starting point of phase semantics is the notion of ''duality''. The structure needed to talk about duality is very simple: one just needs a relation <math>R</math> between two sets <math>X</math> and <math>Y</math>. Using standard mathematical practice, we can write either <math>(a,b) \in R</math> or <math>a\mathrel{R} b</math> to say that <math>a\in X</math> and <math>b\in Y</math> are related. |
||
| Line 15: | Line 16: | ||
{{Definition| |
{{Definition| |
||
If <math>R\subseteq X\times Y</math> is a relation, we write <math>R^\sim\subseteq Y\times X</math> for the converse relation: <math>(b,a)\in R^\sim</math> iff <math>(a,b)\in R</math>. |
If <math>R\subseteq X\times Y</math> is a relation, we write <math>R^\sim\subseteq Y\times X</math> for the converse relation: <math>(b,a)\in R^\sim</math> iff <math>(a,b)\in R</math>. |
||
| + | }} |
||
| − | + | Such a relation yields three interesting operators sending subsets of <math>X</math> to subsets of <math>Y</math>: |
|
| − | Such a relation yields three interesting operators acting on subsets of <math>Y</math>: |
||
{{Definition| |
{{Definition| |
||
Let <math>R\subseteq X\times Y</math> be a relation, define the operators <math>\langle R\rangle</math>, <math>[R]</math> and <math>\_^R</math> taking subsets of <math>X</math> to subsets of <math>Y</math> as follows: |
Let <math>R\subseteq X\times Y</math> be a relation, define the operators <math>\langle R\rangle</math>, <math>[R]</math> and <math>\_^R</math> taking subsets of <math>X</math> to subsets of <math>Y</math> as follows: |
||
| − | # <math>b\in\langle R\rangle(x)</math> iff <math>\exists a\in X,\ (a,b)\in R \land a\in x</math> |
+ | # <math>b\in\langle R\rangle(x)</math> iff <math>\exists a\in x,\ (a,b)\in R</math> |
| − | # <math>b\in[R](x)</math> iff <math>\forall a\in Y,\ (a,b)\in R \implies a\in x</math> |
+ | # <math>b\in[R](x)</math> iff <math>\forall a\in X,\ (a,b)\in R \implies a\in x</math> |
# <math>b\in x^R</math> iff <math>\forall a\in x, (a,b)\in R</math> |
# <math>b\in x^R</math> iff <math>\forall a\in x, (a,b)\in R</math> |
||
}} |
}} |
||
| − | The operator <math>\langle R\rangle</math> is usually called the direct image of the relation, <math>[R]</math> is sometimes called the universal image of the relation. |
+ | The operator <math>\langle R\rangle</math> is usually called the ''direct image'' of the relation, <math>[R]</math> is sometimes called the ''universal image'' of the relation. |
It is trivial to check that <math>\langle R\rangle</math> and <math>[R]</math> are covariant (increasing for the <math>\subseteq</math> relation) while <math>\_^R</math> is contravariant (decreasing for the <math>\subseteq</math> relation). More interesting: |
It is trivial to check that <math>\langle R\rangle</math> and <math>[R]</math> are covariant (increasing for the <math>\subseteq</math> relation) while <math>\_^R</math> is contravariant (decreasing for the <math>\subseteq</math> relation). More interesting: |
||
| Line 36: | Line 38: | ||
This implies directly that <math>\langle R\rangle</math> commutes with arbitrary unions and <math>[R]</math> commutes with arbitrary intersections. (And in fact, any operator commuting with arbitrary unions (resp. intersections) is of the form <math>\langle R\rangle</math> (resp. <math>[R]</math>). |
This implies directly that <math>\langle R\rangle</math> commutes with arbitrary unions and <math>[R]</math> commutes with arbitrary intersections. (And in fact, any operator commuting with arbitrary unions (resp. intersections) is of the form <math>\langle R\rangle</math> (resp. <math>[R]</math>). |
||
| − | ::''Remark: '' the operator <math>\_^R</math> sends unions to intersections because <math>\_^R : \mathcal{P}(X) \to \mathcal{P}(Y)^\mathrm{op}</math> is right adjoint to <math>\_^{R^\sim} : \mathcal{P}(Y)^{\mathrm{op}} \to \mathcal{P}(X)</math>... |
+ | {{Remark|the operator <math>\_^R</math> sends unions to intersections because <math>\_^R : \mathcal{P}(X) \to \mathcal{P}(Y)^\mathrm{op}</math> is right adjoint to <math>\_^{R^\sim} : \mathcal{P}(Y)^{\mathrm{op}} \to \mathcal{P}(X)</math>...}} |
| − | + | ===Closure operators=== |
|
| − | |||
| − | ==Closure operators== |
||
{{Definition| |
{{Definition| |
||
| − | A closure operator on <math>\mathcal{P}(X)</math> is an monotonic increasing operator <math>P</math> on the subsets of <math>X</math> which satisfies: |
+ | A closure operator on <math>\mathcal{P}(X)</math> is a monotonic operator <math>P</math> on the subsets of <math>X</math> which satisfies: |
# for all <math>x\subseteq X</math>, we have <math>x\subseteq P(x)</math> |
# for all <math>x\subseteq X</math>, we have <math>x\subseteq P(x)</math> |
||
# for all <math>x\subseteq X</math>, we have <math>P(P(x))\subseteq P(x)</math> |
# for all <math>x\subseteq X</math>, we have <math>P(P(x))\subseteq P(x)</math> |
||
| Line 48: | Line 50: | ||
Closure operators are quite common in mathematics and computer science. They correspond exactly to the notion of ''monad'' on a preorder... |
Closure operators are quite common in mathematics and computer science. They correspond exactly to the notion of ''monad'' on a preorder... |
||
| + | It follows directly from the definition that for any closure operator <math>P</math>, the image <math>P(x)</math> is a fixed point of <math>P</math>. Moreover: |
||
| + | |||
| + | {{Lemma| |
||
| + | <math>P(x)</math> is the smallest fixed point of <math>P</math> containing <math>x</math>. |
||
| + | }} |
||
| + | |||
| + | One other important property is the following: |
||
{{Lemma| |
{{Lemma| |
||
Write <math>\mathcal{F}(P) = \{x\ |\ P(x)\subseteq x\}</math> for the collection of fixed points of a closure operator <math>P</math>. We have that <math>\left(\mathcal{F}(P),\bigcap\right)</math> is a complete inf-lattice. |
Write <math>\mathcal{F}(P) = \{x\ |\ P(x)\subseteq x\}</math> for the collection of fixed points of a closure operator <math>P</math>. We have that <math>\left(\mathcal{F}(P),\bigcap\right)</math> is a complete inf-lattice. |
||
}} |
}} |
||
| + | |||
| + | {{Remark| |
||
| + | A closure operator is in fact determined by its set of fixed points: we have <math>P(x) = \bigcup \{ y\ |\ y\in\mathcal{F}(P),\,y\subseteq x\}</math>}} |
||
Since any complete inf-lattice is automatically a complete sup-lattice, <math>\mathcal{F}(P)</math> is also a complete sup-lattice. However, the sup operation isn't given by plain union: |
Since any complete inf-lattice is automatically a complete sup-lattice, <math>\mathcal{F}(P)</math> is also a complete sup-lattice. However, the sup operation isn't given by plain union: |
||
{{Lemma| |
{{Lemma| |
||
| − | If <math>P</math> is a closure operator on <math>\mathcal{P}(X)</math>, and if <math>(x_i)_(i\in I)</math> is a (possibly infinite) family of subsets of <math>X</math>, we write <math>\bigvee_{i\in I} x_i = P\left(\bigcup_{i\in I} x_i\right)</math>. |
+ | If <math>P</math> is a closure operator on <math>\mathcal{P}(X)</math>, and if <math>(x_i)_{i\in I}</math> is a (possibly infinite) family of subsets of <math>X</math>, we write <math>\bigvee_{i\in I} x_i = P\left(\bigcup_{i\in I} x_i\right)</math>. |
We have <math>\left(\mathcal{F}(P),\bigcap,\bigvee\right)</math> is a complete lattice. |
We have <math>\left(\mathcal{F}(P),\bigcap,\bigvee\right)</math> is a complete lattice. |
||
| Line 80: | Line 92: | ||
}} |
}} |
||
| − | ::''Remark:'' everything gets a little simpler when <math>R</math> is a symmetric relation on <math>X</math>. |
+ | {{Remark|everything gets a little simpler when <math>R</math> is a symmetric relation on <math>X</math>.}} |
| + | ==Phase Semantics== |
||
| − | + | ===Phase spaces=== |
|
| − | =Phase Semantics= |
||
| − | |||
| − | |||
| − | ==Phase spaces== |
||
{{Definition|title=monoid| |
{{Definition|title=monoid| |
||
| Line 95: | Line 108: | ||
A phase space is given by: |
A phase space is given by: |
||
# a commutative monoid <math>(X,1,\cdot)</math>, |
# a commutative monoid <math>(X,1,\cdot)</math>, |
||
| − | # together with a subset <math>\bot\!\!\!\bot\subseteq X</math>. |
+ | # together with a subset <math>\Bot\subseteq X</math>. |
The elements of <math>X</math> are called ''phases''. |
The elements of <math>X</math> are called ''phases''. |
||
| − | We write <math>\bot</math> for the relation <math>\{(a,b)\ |\ a\cdot b \in \bot\!\!\!\bot\}</math>. This relation is symmetric. |
+ | We write <math>\bot</math> for the relation <math>\{(a,b)\ |\ a\cdot b \in \Bot\}</math>. This relation is symmetric. |
| − | A ''fact'' in a phase space is simply a fixed point for the closure operator <math>x\mapsto x^{\bot\bot}</math>. |
+ | A ''fact'' in a phase space is simply a fixed point for the closure operator <math>x\mapsto x\biorth</math>. |
}} |
}} |
||
| Line 108: | Line 121: | ||
{{Corollary| |
{{Corollary| |
||
The set of facts of a phase space is a complete lattice where: |
The set of facts of a phase space is a complete lattice where: |
||
| − | # <math>\bigwedge</math> is simply <math>\bigcap</math>, |
+ | # <math>\bigwedge_{i\in I} x_i</math> is simply <math>\bigcap_{i\in I} x_i</math>, |
| − | # <math>\bigvee</math> is <math>\left(\bigcup ...\right)^{\bot\bot}</math>. |
+ | # <math>\bigvee_{i\in I} x_i</math> is <math>\left(\bigcup_{i\in I} x_i\right)\biorth</math>. |
}} |
}} |
||
| − | + | ===Additive connectives=== |
|
| − | ==Additive connectives== |
||
The previous corollary makes the following definition correct: |
The previous corollary makes the following definition correct: |
||
{{Definition|title=additive connectives| |
{{Definition|title=additive connectives| |
||
| − | If <math>(X,1,\cdot,\bot\!\!\bot</math> is a phase space, we define the following facts and operations on facts: |
+ | If <math>(X,1,\cdot,\Bot)</math> is a phase space, we define the following facts and operations on facts: |
| − | # <math>\top = X = \emptyset^\bot</math> |
+ | # <math>\top = X = \emptyset\orth</math> |
| − | # <math>\zero = \emptyset^{\bot\bot} = X^\bot</math> |
+ | # <math>\zero = \emptyset\biorth = X\orth</math> |
| − | # <math>x\plus y = (x\cup y)^{\bot\bot}</math> |
||
# <math>x\with y = x\cap y</math> |
# <math>x\with y = x\cap y</math> |
||
| + | # <math>x\plus y = (x\cup y)\biorth</math> |
||
}} |
}} |
||
| Line 127: | Line 141: | ||
{{Lemma|title=additive de Morgan laws| |
{{Lemma|title=additive de Morgan laws| |
||
We have |
We have |
||
| − | # <math>\zero^\bot = \top</math> |
+ | # <math>\zero\orth = \top</math> |
| − | # <math>\top^\bot = \zero</math> |
+ | # <math>\top\orth = \zero</math> |
| − | # <math>(x\plus y)^\bot = x^\bot \with y^\bot</math> |
+ | # <math>(x\with y)\orth = x\orth \plus y\orth</math> |
| − | # <math>(x\with y)^\bot = x^\bot \plus y^\bot</math> |
+ | # <math>(x\plus y)\orth = x\orth \with y\orth</math> |
}} |
}} |
||
| + | ===Multiplicative connectives=== |
||
| + | |||
| + | In order to define the multiplicative connectives, we actually need to use the monoid structure of our phase space. One interpretation that is reminiscent in phase semantics is that our spaces are collections of ''tests'' / programs / proofs / ''strategies'' that can interact with each other. The result of the interaction between <math>a</math> and <math>b</math> is simply <math>a\cdot b</math>. |
||
| + | |||
| + | The set <math>\Bot</math> can be thought of as the set of "good" things, and we thus have <math>a\in x\orth</math> iff "<math>a</math> interacts correctly with all the elements of <math>x</math>". |
||
| + | |||
| + | |||
| + | {{Definition| |
||
| + | If <math>x</math> and <math>y</math> are two subsets of a phase space, we write <math>x\cdot y</math> for the set <math>\{a\cdot b\ |\ a\in x, b\in y\}</math>. |
||
| + | }} |
||
| + | Thus <math>x\cdot y</math> contains all the possible interactions between one element of <math>x</math> and one element of <math>y</math>. |
||
| + | |||
| + | |||
| + | The tensor connective of linear logic is now defined as: |
||
| + | |||
| + | {{Definition| title=multiplicative connectives| |
||
| + | If <math>x</math> and <math>y</math> are facts in a phase space, we define |
||
| + | * <math>\one = \{1\}\biorth</math>; |
||
| + | * <math>\bot = \one\orth</math>; |
||
| + | * the tensor <math>x\tens y</math> to be the fact <math>(x\cdot y)\biorth</math>; |
||
| + | * the par connective is the de Morgan dual of the tensor: <math>x\parr y = (x\orth \tens y\orth)\orth</math>; |
||
| + | * the linear arrow is just <math>x\limp y = x\orth\parr y = (x\tens y\orth)\orth</math>. |
||
| + | }} |
||
| + | |||
| + | Note that by unfolding the definition of <math>\limp</math>, we have the following, "intuitive" definition of <math>x\limp y</math>: |
||
| + | |||
| + | {{Lemma| |
||
| + | If <math>x</math> and <math>y</math> are facts, we have <math>a\in x\limp y</math> iff <math>\forall b\in x,\,a\cdot b\in y</math> |
||
| + | }} |
||
| + | |||
| + | {{Proof| |
||
| + | easy exercise. }} |
||
| + | |||
| + | Readers familiar with realisability will appreciate... |
||
| + | |||
| + | {{Remark| |
||
| + | Some people say that this idea of orthogonality was implicitly present in Tait's proof of strong normalisation. More recently, Jean-Louis Krivine and Alexandre Miquel have used the idea explicitly to do realisability...}} |
||
| + | |||
| + | |||
| + | ===Properties=== |
||
| + | |||
| + | All the expected properties hold: |
||
| + | |||
| + | {{Lemma| |
||
| + | * The operations <math>\tens</math>, <math>\parr</math>, <math>\plus</math> and <math>\with</math> are commutative and associative, |
||
| + | * They have respectively <math>\one</math>, <math>\bot</math>, <math>\zero</math> and <math>\top</math> as neutral element, |
||
| + | * <math>\zero</math> is absorbing for <math>\tens</math>, |
||
| + | * <math>\top</math> is absorbing for <math>\parr</math>, |
||
| + | * <math>\tens</math> distributes over <math>\plus</math>, |
||
| + | * <math>\parr</math> distributes over <math>\with</math>. |
||
| + | }} |
||
| + | |||
| + | ===Exponentials=== |
||
| + | |||
| + | {{Definition|title=Exponentials| |
||
| + | Write <math>I</math> for the set of idempotents of a phase space: <math>I=\{a\ |\ a\cdot a=a\}</math>. We put: |
||
| + | # <math>\oc x = (x\cap I\cap \one)\biorth</math>, |
||
| + | # <math>\wn x = (x\orth\cap I\cap\one)\orth</math>. |
||
| + | }} |
||
| + | |||
| + | This definition captures precisely the intuition behind the exponentials: |
||
| + | * we need to have contraction, hence we restrict to indempotents in <math>x</math>, |
||
| + | * and weakening, hence we restrict to <math>\one</math>. |
||
| + | Since <math>I</math> isn't necessarily a fact, we then take the biorthogonal to get a fact... |
||
| + | |||
| + | == Soundness == |
||
| + | |||
| + | {{Definition|Let <math>(X, 1, \cdot)</math> be a commutative monoid. |
||
| + | |||
| + | Given a formula <math>A</math> of linear logic and an assignation <math>\rho</math> that associate a fact to any variable, we can inductively define the interpretation <math>\sem{A}_\rho</math> of <math>A</math> in <math>X</math> as one would expect. Interpretation is lifted to sequents as <math>\sem{A_1, \dots, A_n}_\rho = \sem{A_1}_\rho \parr \cdots \parr \sem{A_n}_\rho</math>.}} |
||
| + | |||
| + | {{Theorem|Let <math>\Gamma</math> be a provable sequent in linear logic. Then <math>1_X \in \sem{\Gamma}</math>.}} |
||
| + | |||
| + | {{Proof|By induction on <math>\vdash\Gamma</math>.}} |
||
| + | |||
| + | == Completeness == |
||
| + | |||
| + | Phase semantics is complete w.r.t. linear logic. In order to prove this, we need to build a particular commutative monoid. |
||
| + | |||
| + | {{Definition|We define the '''syntactic monoid''' as follows: |
||
| + | |||
| + | * Its elements are sequents <math>\Gamma</math> quotiented by the equivalence relation <math>\cong</math> generated by the rules: |
||
| + | *# <math>\Gamma \cong \Delta</math> if <math>\Gamma</math> is a permutation of <math>\Delta</math> |
||
| + | *# <math>\wn{A}, \wn{A}, \Gamma \cong \wn{A}, \Gamma</math> |
||
| + | |||
| + | * Product is concatenation: <math>\Gamma \cdot \Delta := \Gamma, \Delta</math> |
||
| + | * Neutral element is the empty sequent: <math>1 := \emptyset</math>.}} |
||
| − | ==Multiplicative connectives== |
+ | The equivalence relation intuitively means that we do not care about the multiplicity of <math>\wn</math>-formulae. |
| − | In order to define the multiplicative connectives, we actually need to use the monoid structure of our phase space. |
+ | {{Lemma|The syntactic monoid is indeed a commutative monoid.}} |
| + | {{Definition|The '''syntactic assignation''' is the assignation that sends any variable <math>\alpha</math> to the fact <math>\{\alpha\}\orth</math>.}} |
||
| − | --- TODO --- |
+ | We instantiate the pole as <math>\Bot := \{\Gamma \mid \vdash\Gamma\}</math>. |
| + | {{Theorem|If <math>\Gamma\in\sem{\Gamma}\orth</math>, then <math>\vdash\Gamma</math>.}} |
||
| − | ==Exponentials== |
+ | {{Proof|By induction on <math>\Gamma</math>.}} |
| + | == Cut elimination == |
||
| + | Actually, the completeness result is stronger, as the proof does not use the cut-rule in the reconstruction of <math>\vdash\Gamma</math>. By refining the pole as the set of ''cut-free'' provable formulae, we get: |
||
| − | =Completeness= |
+ | {{Theorem|If <math>\Gamma\in\sem{\Gamma}\orth</math>, then <math>\Gamma</math> is cut-free provable.}} |
| + | From soundness, one can retrieve the cut-elimination theorem. |
||
| + | {{Corollary|Linear logic enjoys the cut-elimination property.}} |
||
| − | =The Rest= |
+ | ==The Rest== |
Latest revision as of 14:55, 22 January 2020
Contents |
[edit] Introduction
The semantics given by phase spaces is a kind of "formula and provability semantics", and is thus quite different in spirit from the more usual denotational semantics of linear logic. (Those are rather some "formulas and proofs semantics".)
--- probably a whole lot more of blabla to put here... ---
[edit] Preliminaries: relation and closure operators
Part of the structure obtained from phase semantics works in a very general framework and relies solely on the notion of relation between two sets.
[edit] Relations and operators on subsets
The starting point of phase semantics is the notion of duality. The structure needed to talk about duality is very simple: one just needs a relation R between two sets X and Y. Using standard mathematical practice, we can write either 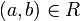 or
or 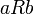 to say that
to say that 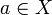 and
and 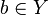 are related.
are related.
Definition
If 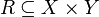 is a relation, we write
is a relation, we write 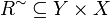 for the converse relation:
for the converse relation: 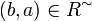 iff
iff 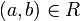 .
.
Such a relation yields three interesting operators sending subsets of X to subsets of Y:
Definition
Let 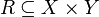 be a relation, define the operators
be a relation, define the operators 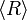 , [R] and _R taking subsets of X to subsets of Y as follows:
, [R] and _R taking subsets of X to subsets of Y as follows:
-
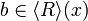 iff
iff 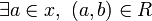
-
](/mediawiki/images/math/d/0/7/d07a7a5791bf9a30f7930c3262374a63.png) iff
iff 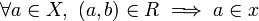
-
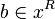 iff
iff 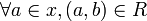
The operator 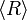 is usually called the direct image of the relation, [R] is sometimes called the universal image of the relation.
is usually called the direct image of the relation, [R] is sometimes called the universal image of the relation.
It is trivial to check that 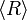 and [R] are covariant (increasing for the
and [R] are covariant (increasing for the 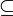 relation) while _R is contravariant (decreasing for the
relation) while _R is contravariant (decreasing for the 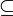 relation). More interesting:
relation). More interesting:
Lemma (Galois Connections)
-
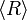 is right-adjoint to [R˜]: for any
is right-adjoint to [R˜]: for any 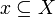 and
and 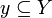 , we have
, we have ![[R^\sim]y \subseteq x](/mediawiki/images/math/e/c/8/ec870ce68fdcd3a37af2e07d062e18e6.png) iff
iff 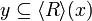
- we have
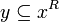 iff
iff 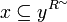
This implies directly that 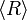 commutes with arbitrary unions and [R] commutes with arbitrary intersections. (And in fact, any operator commuting with arbitrary unions (resp. intersections) is of the form
commutes with arbitrary unions and [R] commutes with arbitrary intersections. (And in fact, any operator commuting with arbitrary unions (resp. intersections) is of the form 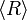 (resp. [R]).
(resp. [R]).
Remark: the operator _R sends unions to intersections because 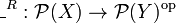 is right adjoint to
is right adjoint to 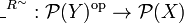 ...
...
[edit] Closure operators
Definition
A closure operator on 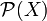 is a monotonic operator P on the subsets of X which satisfies:
is a monotonic operator P on the subsets of X which satisfies:
- for all
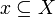 , we have
, we have 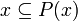
- for all
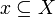 , we have
, we have 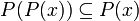
Closure operators are quite common in mathematics and computer science. They correspond exactly to the notion of monad on a preorder...
It follows directly from the definition that for any closure operator P, the image P(x) is a fixed point of P. Moreover:
Lemma
P(x) is the smallest fixed point of P containing x.
One other important property is the following:
Lemma
Write 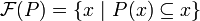 for the collection of fixed points of a closure operator P. We have that
for the collection of fixed points of a closure operator P. We have that 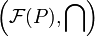 is a complete inf-lattice.
is a complete inf-lattice.
Remark:
A closure operator is in fact determined by its set of fixed points: we have 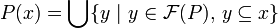
Since any complete inf-lattice is automatically a complete sup-lattice, 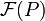 is also a complete sup-lattice. However, the sup operation isn't given by plain union:
is also a complete sup-lattice. However, the sup operation isn't given by plain union:
Lemma
If P is a closure operator on 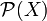 , and if
, and if 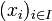 is a (possibly infinite) family of subsets of X, we write
is a (possibly infinite) family of subsets of X, we write 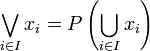 .
.
We have 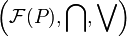 is a complete lattice.
is a complete lattice.
Proof. easy.
A rather direct consequence of the Galois connections of the previous section is:
Lemma
The operator and ![\langle R\rangle \circ [R^\sim]](/mediawiki/images/math/9/8/3/98308747bc920bef92643b3fcc53ee83.png) and the operator
and the operator 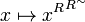 are closures.
are closures.
A last trivial lemma:
Lemma
We have 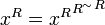 .
.
As a consequence, a subset 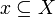 is in
is in 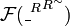 iff it is of the form
iff it is of the form 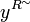 .
.
Remark: everything gets a little simpler when R is a symmetric relation on X.
[edit] Phase Semantics
[edit] Phase spaces
Definition (monoid)
A monoid is simply a set X equipped with a binary operation  s.t.:
s.t.:
- the operation is associative
- there is a neutral element
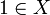
The monoid is commutative when the binary operation is commutative.
Definition (Phase space)
A phase space is given by:
- a commutative monoid
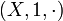 ,
,
- together with a subset
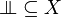 .
.
The elements of X are called phases.
We write 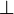 for the relation
for the relation 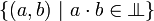 . This relation is symmetric.
. This relation is symmetric.
A fact in a phase space is simply a fixed point for the closure operator 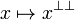 .
.
Thanks to the preliminary work, we have:
Corollary
The set of facts of a phase space is a complete lattice where:
-
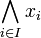 is simply
is simply 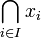 ,
,
-
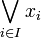 is
is 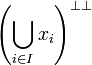 .
.
[edit] Additive connectives
The previous corollary makes the following definition correct:
Definition (additive connectives)
If 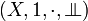 is a phase space, we define the following facts and operations on facts:
is a phase space, we define the following facts and operations on facts:
Once again, the next lemma follows from previous observations:
Lemma (additive de Morgan laws)
We have
[edit] Multiplicative connectives
In order to define the multiplicative connectives, we actually need to use the monoid structure of our phase space. One interpretation that is reminiscent in phase semantics is that our spaces are collections of tests / programs / proofs / strategies that can interact with each other. The result of the interaction between a and b is simply 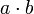 .
.
The set 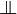 can be thought of as the set of "good" things, and we thus have
can be thought of as the set of "good" things, and we thus have 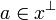 iff "a interacts correctly with all the elements of x".
iff "a interacts correctly with all the elements of x".
Definition
If x and y are two subsets of a phase space, we write 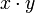 for the set
for the set 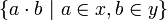 .
.
Thus 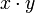 contains all the possible interactions between one element of x and one element of y.
contains all the possible interactions between one element of x and one element of y.
The tensor connective of linear logic is now defined as:
Definition (multiplicative connectives)
If x and y are facts in a phase space, we define
-
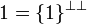 ;
;
-
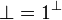 ;
;
- the tensor
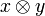 to be the fact
to be the fact 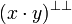 ;
;
- the par connective is the de Morgan dual of the tensor:
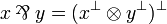 ;
;
- the linear arrow is just
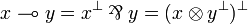 .
.
Note that by unfolding the definition of 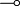 , we have the following, "intuitive" definition of
, we have the following, "intuitive" definition of 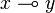 :
:
Lemma
If x and y are facts, we have 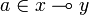 iff
iff 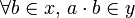
Proof. easy exercise.
Readers familiar with realisability will appreciate...
Remark:
Some people say that this idea of orthogonality was implicitly present in Tait's proof of strong normalisation. More recently, Jean-Louis Krivine and Alexandre Miquel have used the idea explicitly to do realisability...
[edit] Properties
All the expected properties hold:
Lemma
- The operations
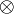 ,
, 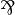 ,
, 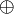 and
and 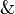 are commutative and associative,
are commutative and associative,
- They have respectively
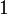 ,
, 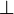 ,
, 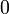 and
and 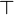 as neutral element,
as neutral element,
-
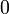 is absorbing for
is absorbing for 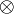 ,
,
-
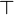 is absorbing for
is absorbing for 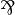 ,
,
-
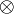 distributes over
distributes over 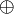 ,
,
-
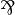 distributes over
distributes over 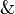 .
.
[edit] Exponentials
Definition (Exponentials)
Write I for the set of idempotents of a phase space: 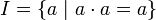 . We put:
. We put:
-
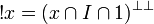 ,
,
-
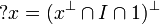 .
.
This definition captures precisely the intuition behind the exponentials:
- we need to have contraction, hence we restrict to indempotents in x,
- and weakening, hence we restrict to
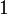 .
.
Since I isn't necessarily a fact, we then take the biorthogonal to get a fact...
[edit] Soundness
Definition
Let 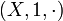 be a commutative monoid.
be a commutative monoid.
Given a formula A of linear logic and an assignation ρ that associate a fact to any variable, we can inductively define the interpretation 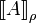 of A in X as one would expect. Interpretation is lifted to sequents as
of A in X as one would expect. Interpretation is lifted to sequents as 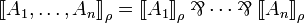 .
.
Theorem
Let Γ be a provable sequent in linear logic. Then 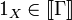 .
.
Proof. By induction on 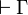 .
.
[edit] Completeness
Phase semantics is complete w.r.t. linear logic. In order to prove this, we need to build a particular commutative monoid.
Definition
We define the syntactic monoid as follows:
- Its elements are sequents Γ quotiented by the equivalence relation
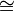 generated by the rules:
generated by the rules:
-
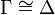 if Γ is a permutation of Δ
if Γ is a permutation of Δ
-
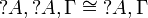
-
- Product is concatenation:
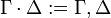
- Neutral element is the empty sequent:
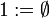 .
.
The equivalence relation intuitively means that we do not care about the multiplicity of 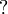 -formulae.
-formulae.
Lemma
The syntactic monoid is indeed a commutative monoid.
Definition
The syntactic assignation is the assignation that sends any variable α to the fact 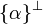 .
.
We instantiate the pole as 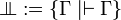 .
.
Theorem
If 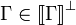 , then
, then 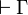 .
.
Proof. By induction on Γ.
[edit] Cut elimination
Actually, the completeness result is stronger, as the proof does not use the cut-rule in the reconstruction of 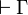 . By refining the pole as the set of cut-free provable formulae, we get:
. By refining the pole as the set of cut-free provable formulae, we get:
Theorem
If 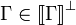 , then Γ is cut-free provable.
, then Γ is cut-free provable.
From soundness, one can retrieve the cut-elimination theorem.
Corollary
Linear logic enjoys the cut-elimination property.