List of equivalences
From LLWiki
(Difference between revisions)
(First list of equivalences) |
m (Correction of useless corrections) |
||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Each [[List of isomorphisms|isomorphism]] gives an equivalence of formulas. |
Each [[List of isomorphisms|isomorphism]] gives an equivalence of formulas. |
||
| − | The following equivalences are not isomorphisms. |
+ | The following equivalences are ''not'' isomorphisms. |
| + | |||
| + | == Multiplicatives == |
||
| + | |||
| + | <math> |
||
| + | \begin{array}{rcccl} |
||
| + | A &\linequiv& A \tens (A\orth\parr A) &\linequiv& (A\tens A\orth)\parr A \\ |
||
| + | & & A\parr A\orth &\linequiv& (A\parr A\orth)\tens(A\parr A\orth) |
||
| + | \end{array} |
||
| + | </math> |
||
== Additives == |
== Additives == |
||
| Line 22: | Line 22: | ||
\end{array} |
\end{array} |
||
</math> |
</math> |
||
| + | |||
| + | == Exponentials == |
||
| + | |||
| + | <math> |
||
| + | \begin{array}{rclcrcl} |
||
| + | \oc A &\linequiv& \oc A\tens\oc A &\quad& |
||
| + | \wn A &\linequiv& \wn A\parr\wn A\\ |
||
| + | \oc A &\linequiv& \oc\oc A &\quad& \wn A &\linequiv& \wn\wn A\\ |
||
| + | \oc\wn A &\linequiv& \oc\wn\oc\wn A &\quad& \wn\oc A &\linequiv& \wn\oc\wn\oc A\\ |
||
| + | \end{array} |
||
| + | </math> |
||
| + | |||
| + | Some of these equivalences are related with the [[lattice of exponential modalities]]. |
||
== Polarities == |
== Polarities == |
||
| Line 61: | Line 74: | ||
<math> |
<math> |
||
\begin{array}{rcl} |
\begin{array}{rcl} |
||
| + | \one &\linequiv& \oc{(A\orth\parr A)} \\ |
||
| + | \bot &\linequiv& \wn{(A\orth\tens A)} \\ |
||
| + | \\ |
||
\oc{\wn{(\oc{A}\with\oc{B})}} &\linequiv& \oc{(\wn{\oc{A}}\with\wn{\oc{B}})} \\ |
\oc{\wn{(\oc{A}\with\oc{B})}} &\linequiv& \oc{(\wn{\oc{A}}\with\wn{\oc{B}})} \\ |
||
\wn{\oc{(\wn{A}\plus\wn{B})}} &\linequiv& \wn{(\oc{\wn{A}}\plus\oc{\wn{B}})} |
\wn{\oc{(\wn{A}\plus\wn{B})}} &\linequiv& \wn{(\oc{\wn{A}}\plus\oc{\wn{B}})} |
||
Latest revision as of 21:03, 27 July 2017
Each isomorphism gives an equivalence of formulas. The following equivalences are not isomorphisms.
Contents |
[edit] Multiplicatives

[edit] Additives
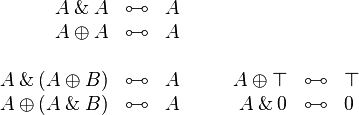
[edit] Quantifiers
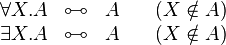
[edit] Exponentials
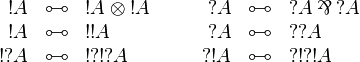
Some of these equivalences are related with the lattice of exponential modalities.
[edit] Polarities
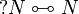
|
(N negative) |
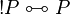
|
(P positive) |
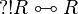
|
(R regular) |
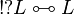
|
(L co-regular) |
[edit] Second order encodings
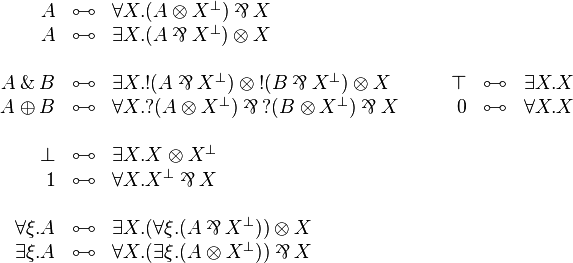
[edit] Miscellaneous