Lattice of exponential modalities
(lattice drawing only) |
m (Pointer to list of equivalences) |
||
| (5 intermediate revisions by one user not shown) | |||
| Line 3: | Line 3: | ||
& & {\wn} \\ |
& & {\wn} \\ |
||
& & & & {\wn\oc\wn}\ar[ull] \\ |
& & & & {\wn\oc\wn}\ar[ull] \\ |
||
| − | \emptyset\ar[uurr] & & & {\oc\wn} \ar[ur] & & {\wn\oc} \ar[ul] \\ |
+ | \varepsilon\ar[uurr] & & & {\oc\wn} \ar[ur] & & {\wn\oc} \ar[ul] \\ |
& & & & {\oc\wn\oc} \ar[ul]\ar[ur] \\ |
& & & & {\oc\wn\oc} \ar[ul]\ar[ur] \\ |
||
& & {\oc} \ar[uull]\ar[urr] |
& & {\oc} \ar[uull]\ar[urr] |
||
} |
} |
||
</math> |
</math> |
||
| + | |||
| + | An ''exponential modality'' is an arbitrary (possibly empty) sequence of the two exponential connectives <math>\oc</math> and <math>\wn</math>. It can be considered itself as a unary connective. This leads to the notation <math>\mu A</math> for applying an exponential modality <math>\mu</math> to a formula <math>A</math>. |
||
| + | |||
| + | There is a preorder relation on exponential modalities defined by <math>\mu\lesssim\nu</math> if and only if for any formula <math>A</math> we have <math>\mu A\vdash \nu A</math>. It induces an [[List of equivalences|equivalence]] relation on exponential modalities by <math>\mu \sim \nu</math> if and only if <math>\mu\lesssim\nu</math> and <math>\nu\lesssim\mu</math>. |
||
| + | |||
| + | {{Lemma| |
||
| + | For any formula <math>A</math>, <math>\oc{A}\vdash A</math> and <math>A\vdash\wn{A}</math>. |
||
| + | }} |
||
| + | |||
| + | {{Lemma|title=Functoriality| |
||
| + | If <math>A</math> and <math>B</math> are two formulas such that <math>A\vdash B</math> then, for any exponential modality <math>\mu</math>, <math>\mu A\vdash \mu B</math>. |
||
| + | }} |
||
| + | |||
| + | {{Lemma| |
||
| + | For any formula <math>A</math>, <math>\oc{A}\vdash \oc{\oc{A}}</math> and <math>\wn{\wn{A}}\vdash\wn{A}</math>. |
||
| + | }} |
||
| + | |||
| + | {{Lemma| |
||
| + | For any formula <math>A</math>, <math>\oc{A}\vdash \oc{\wn{\oc{A}}}</math> and <math>\wn{\oc{\wn{A}}}\vdash\wn{A}</math>. |
||
| + | }} |
||
| + | |||
| + | This allows to prove that any exponential modality is equivalent to one of the following seven modalities: <math>\varepsilon</math> (the empty modality), <math>\oc</math>, <math>\wn</math>, <math>\oc\wn</math>, <math>\wn\oc</math>, <math>\oc\wn\oc</math> or <math>\wn\oc\wn</math>. |
||
| + | Indeed any sequence of consecutive <math>\oc</math> or <math>\wn</math> in a modality can be simplified into only one occurrence, and then any alternating sequence of length at least four can be simplified into a smaller one. |
||
| + | |||
| + | {{Proof| |
||
| + | We obtain <math>\oc{\oc{A}}\vdash\oc{A}</math> by functoriality from <math>\oc{A}\vdash A</math> (and similarly for <math>\wn{A}\vdash\wn{\wn{A}}</math>). |
||
| + | From <math>\oc{A}\vdash \oc{\wn{\oc{A}}}</math>, we deduce <math>\wn{\oc{A}}\vdash \wn{\oc{\wn{\oc{A}}}}</math> by functoriality and <math>\oc{\wn{B}}\vdash \oc{\wn{\oc{\wn{B}}}}</math> (with <math>A=\wn{B}</math>). In a similar way we have <math>\oc{\wn{\oc{\wn{A}}}}\vdash \oc{\wn{A}}</math> and <math>\wn{\oc{\wn{\oc{A}}}}\vdash \wn{\oc{A}}</math>. |
||
| + | }} |
||
| + | |||
| + | The order relation induced on equivalence classes of exponential modalities with respect to <math>\sim</math> can be proved to be the one represented on the picture in the top of this page. All the represented relations are valid. |
||
| + | |||
| + | {{Proof| |
||
| + | We have already seen <math>\oc{A}\vdash A</math> and <math>\oc{A}\vdash \oc{\wn{\oc{A}}}</math>. By functoriality we deduce <math>\oc{\wn{\oc{A}}}\vdash \oc{\wn{A}}</math> and by <math>A=\wn{\oc{B}}</math> we deduce <math>\oc{\wn{\oc{B}}}\vdash \wn{\oc{B}}</math>. |
||
| + | |||
| + | The others are obtained from these ones by duality: <math>A\vdash B</math> entails <math>B\orth\vdash A\orth</math>. |
||
| + | }} |
||
| + | |||
| + | {{Lemma| |
||
| + | If <math>\alpha</math> is an atom, <math>\wn{\alpha}\not\vdash\alpha</math> and |
||
| + | <math>\alpha\not\vdash\wn{\oc{\wn{\alpha}}}</math>. |
||
| + | }} |
||
| + | |||
| + | We can prove that no other relation between classes is true (by relying on the previous lemma). |
||
| + | |||
| + | {{Proof| |
||
| + | From the lemma and <math>A\vdash\wn{A}</math>, we have <math>\wn{\alpha}\not\vdash\wn{\oc{\wn{\alpha}}}</math>. |
||
| + | |||
| + | Then <math>\wn</math> cannot be smaller than any other of the seven modalities (since they are all smaller than <math>\varepsilon</math> or <math>\wn\oc\wn</math>). For the same reason, <math>\varepsilon</math> cannot be smaller than <math>\oc</math>, <math>\oc\wn</math>, <math>\wn\oc</math> or <math>\oc\wn\oc</math>. This entails that <math>\wn\oc\wn</math> is only smaller than <math>\wn</math> since it is not smaller than <math>\varepsilon</math> (by duality from <math>\varepsilon</math> not smaller than <math>\oc\wn\oc</math>). |
||
| + | |||
| + | From these, <math>\wn{\oc{\alpha}}\not\vdash\oc{\wn{\alpha}}</math> and <math>\oc{\wn{\alpha}}\not\vdash\wn{\oc{\alpha}}</math>, we deduce that no other relation is possible. |
||
| + | }} |
||
| + | |||
| + | The order relation on equivalence classes of exponential modalities is a lattice. |
||
Latest revision as of 11:26, 21 November 2014
![\xymatrix{
& & {\wn} \\
& & & & {\wn\oc\wn}\ar[ull] \\
\varepsilon\ar[uurr] & & & {\oc\wn} \ar[ur] & & {\wn\oc} \ar[ul] \\
& & & & {\oc\wn\oc} \ar[ul]\ar[ur] \\
& & {\oc} \ar[uull]\ar[urr]
}](/mediawiki/images/math/e/7/1/e710e498a4904e4aec55029f61ac16da.png)
An exponential modality is an arbitrary (possibly empty) sequence of the two exponential connectives 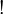 and
and 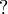 . It can be considered itself as a unary connective. This leads to the notation μA for applying an exponential modality μ to a formula A.
. It can be considered itself as a unary connective. This leads to the notation μA for applying an exponential modality μ to a formula A.
There is a preorder relation on exponential modalities defined by 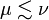 if and only if for any formula A we have
if and only if for any formula A we have 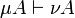 . It induces an equivalence relation on exponential modalities by μ˜ν if and only if
. It induces an equivalence relation on exponential modalities by μ˜ν if and only if 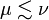 and
and 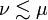 .
.
Lemma
For any formula A, 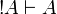 and
and 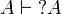 .
.
Lemma (Functoriality)
If A and B are two formulas such that 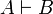 then, for any exponential modality μ,
then, for any exponential modality μ, 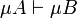 .
.
Lemma
For any formula A, 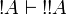 and
and 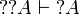 .
.
Lemma
For any formula A, 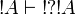 and
and 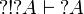 .
.
This allows to prove that any exponential modality is equivalent to one of the following seven modalities:  (the empty modality),
(the empty modality), 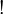 ,
,  ,
, 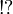 ,
, 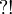 ,
, 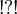 or
or 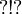 .
Indeed any sequence of consecutive
.
Indeed any sequence of consecutive 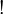 or
or 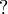 in a modality can be simplified into only one occurrence, and then any alternating sequence of length at least four can be simplified into a smaller one.
in a modality can be simplified into only one occurrence, and then any alternating sequence of length at least four can be simplified into a smaller one.
Proof.
We obtain 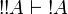 by functoriality from
by functoriality from 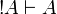 (and similarly for
(and similarly for 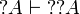 ).
From
).
From 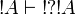 , we deduce
, we deduce 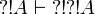 by functoriality and
by functoriality and 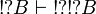 (with
(with 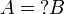 ). In a similar way we have
). In a similar way we have 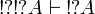 and
and 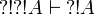 .
.
The order relation induced on equivalence classes of exponential modalities with respect to ˜ can be proved to be the one represented on the picture in the top of this page. All the represented relations are valid.
Proof.
We have already seen 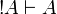 and
and 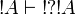 . By functoriality we deduce
. By functoriality we deduce 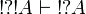 and by
and by 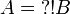 we deduce
we deduce 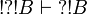 .
.
The others are obtained from these ones by duality: 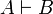 entails
entails 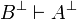 .
.
Lemma
If α is an atom, 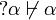 and
and
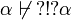 .
.
We can prove that no other relation between classes is true (by relying on the previous lemma).
Proof.
From the lemma and 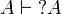 , we have
, we have 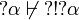 .
.
Then 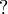 cannot be smaller than any other of the seven modalities (since they are all smaller than
cannot be smaller than any other of the seven modalities (since they are all smaller than  or
or 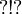 ). For the same reason,
). For the same reason,  cannot be smaller than
cannot be smaller than 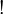 ,
, 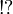 ,
, 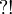 or
or 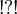 . This entails that
. This entails that 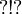 is only smaller than
is only smaller than 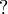 since it is not smaller than
since it is not smaller than  (by duality from
(by duality from  not smaller than
not smaller than 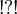 ).
).
From these, 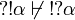 and
and 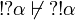 , we deduce that no other relation is possible.
, we deduce that no other relation is possible.
The order relation on equivalence classes of exponential modalities is a lattice.