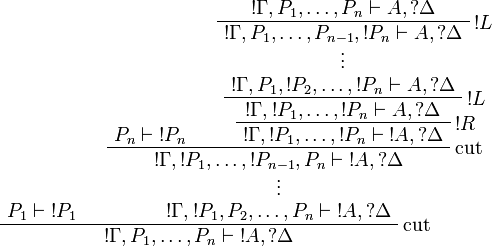Positive formula
m (Updated the 'equivalent' link) |
m (→Generalized structural rules: Link to wikipedia:comoind) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
A ''positive formula'' is a formula <math>P</math> such that <math>P\limp\oc P</math> (thus a [[Wikipedia:F-coalgebra|coalgebra]] for the [[Wikipedia:Comonad|comonad]] <math>\oc</math>). As a consequence <math>P</math> and <math>\oc P</math> are [[Sequent calculus#Equivalences|equivalent]]. |
A ''positive formula'' is a formula <math>P</math> such that <math>P\limp\oc P</math> (thus a [[Wikipedia:F-coalgebra|coalgebra]] for the [[Wikipedia:Comonad|comonad]] <math>\oc</math>). As a consequence <math>P</math> and <math>\oc P</math> are [[Sequent calculus#Equivalences|equivalent]]. |
||
| + | |||
| + | A formula <math>P</math> is positive if and only if <math>P\orth</math> is [[Negative formula|negative]]. |
||
== Positive connectives == |
== Positive connectives == |
||
| Line 121: | Line 123: | ||
== Generalized structural rules == |
== Generalized structural rules == |
||
| − | Positive formulas admit generalized left structural rules corresponding to a structure of <math>\tens</math>-comonoid: <math>P\limp P\tens P</math> and <math>P\limp\one</math>. The following rule is derivable: |
+ | Positive formulas admit generalized left structural rules corresponding to a structure of [[Wikipedia:Comonoid|<math>\tens</math>-comonoid]]: <math>P\limp P\tens P</math> and <math>P\limp\one</math>. The following rule is derivable: |
<math> |
<math> |
||
| Line 178: | Line 180: | ||
\AxRule{\oc\Gamma,P_1,\dots,P_n\vdash A,\wn\Delta} |
\AxRule{\oc\Gamma,P_1,\dots,P_n\vdash A,\wn\Delta} |
||
\LabelRule{\oc L} |
\LabelRule{\oc L} |
||
| − | \UnaRule{\oc\Gamma,P_1,\dots,\oc{P_n}\vdash A,\wn\Delta} |
+ | \UnaRule{\oc\Gamma,P_1,\dots,P_{n-1},\oc{P_n}\vdash A,\wn\Delta} |
| − | \UnaRule{\vdots} |
+ | \VdotsRule{}{\oc\Gamma,P_1,\oc{P_2},\dots,\oc{P_n}\vdash A,\wn\Delta} |
\LabelRule{\oc L} |
\LabelRule{\oc L} |
||
\UnaRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_n}\vdash A,\wn\Delta} |
\UnaRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_n}\vdash A,\wn\Delta} |
||
| Line 185: | Line 187: | ||
\UnaRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_n}\vdash \oc{A},\wn\Delta} |
\UnaRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_n}\vdash \oc{A},\wn\Delta} |
||
\LabelRule{\rulename{cut}} |
\LabelRule{\rulename{cut}} |
||
| − | \BinRule{\oc\Gamma,\oc{P_1},\dots,P_n\vdash \oc{A},\wn\Delta} |
+ | \BinRule{\oc\Gamma,\oc{P_1},\dots,\oc{P_{n-1}},P_n\vdash \oc{A},\wn\Delta} |
| − | \UnaRule{\vdots} |
+ | \VdotsRule{}{\oc\Gamma,\oc{P_1},P_2,\dots,P_n\vdash \oc{A},\wn\Delta} |
\LabelRule{\rulename{cut}} |
\LabelRule{\rulename{cut}} |
||
\BinRule{\oc\Gamma,P_1,\dots,P_n\vdash \oc{A},\wn\Delta} |
\BinRule{\oc\Gamma,P_1,\dots,P_n\vdash \oc{A},\wn\Delta} |
||
Latest revision as of 18:49, 28 October 2013
A positive formula is a formula P such that 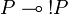 (thus a coalgebra for the comonad
(thus a coalgebra for the comonad 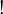 ). As a consequence P and
). As a consequence P and 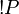 are equivalent.
are equivalent.
A formula P is positive if and only if 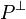 is negative.
is negative.
[edit] Positive connectives
A connective c of arity n is positive if for any positive formulas P1,...,Pn, 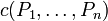 is positive.
is positive.
Proposition (Positive connectives)
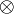 ,
, 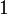 ,
, 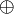 ,
, 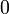 ,
, 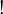 and
and 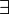 are positive connectives.
are positive connectives.
Proof.
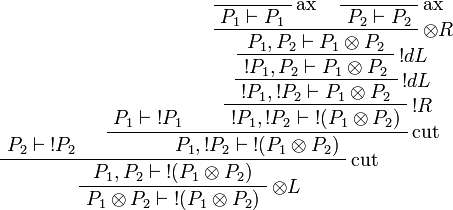
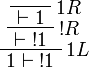
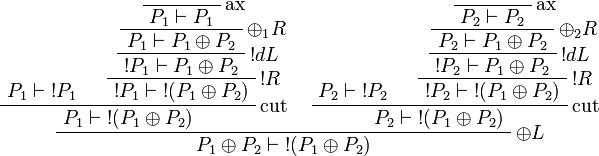
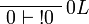
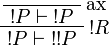
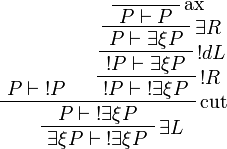
More generally, 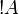 is positive for any formula A.
is positive for any formula A.
The notion of positive connective is related with but different from the notion of asynchronous connective.
[edit] Generalized structural rules
Positive formulas admit generalized left structural rules corresponding to a structure of 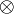 -comonoid:
-comonoid: 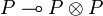 and
and 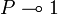 . The following rule is derivable:
. The following rule is derivable:
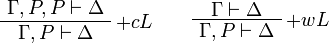
Proof.
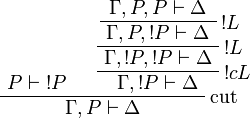
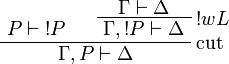
Positive formulas are also acceptable in the left-hand side context of the promotion rule. The following rule is derivable:
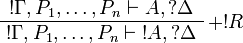
Proof.