Notations
From LLWiki
(Difference between revisions)
Lionel Vaux (Talk | contribs) (→Miscellaneous) |
Lionel Vaux (Talk | contribs) |
||
| Line 68: | Line 68: | ||
* Web of the finiteness space <math>\mathcal A</math>: <math>\web{\mathcal A}</math> |
* Web of the finiteness space <math>\mathcal A</math>: <math>\web{\mathcal A}</math> |
||
* Finiteness structure of the space <math>\mathcal A</math>: <math>\mathfrak F(\mathcal A)</math> (we use <tt>\mathfrak</tt>, which is consistent with the fact that <math>\finpowerset{\web{\mathcal A}}\subseteq \mathfrak F(\mathcal A) \subseteq\powerset{\web{\mathcal A}}</math>). |
* Finiteness structure of the space <math>\mathcal A</math>: <math>\mathfrak F(\mathcal A)</math> (we use <tt>\mathfrak</tt>, which is consistent with the fact that <math>\finpowerset{\web{\mathcal A}}\subseteq \mathfrak F(\mathcal A) \subseteq\powerset{\web{\mathcal A}}</math>). |
||
| + | |||
| + | |||
| + | == [[A formal account of nets|Nets]] == |
||
| + | |||
| + | * The free ports of a net <math>R</math>: <math>\mathrm{fp}(R)</math>. |
||
| + | * The result of the connection of two nets <math>R</math> and <math>R'</math>, given the partial bijection <math>f:\mathrm{fp}(R)\pinj \mathrm{fp}(R')</math>: <math>R\bowtie_f R'</math>. |
||
| + | * The number of loops in the resulting net: <math>\Inner{R}{R'}_f</math> (includes the loops already present in <math>R</math> and <math>R'</math>). |
||
== Miscellaneous == |
== Miscellaneous == |
||
Latest revision as of 12:56, 6 September 2012
Contents |
[edit] Logical systems
For a given logical system such as MLL (for multiplicative linear logic), we consider the following variations:
| Notation | Meaning | Connectives |
|---|---|---|
| MLL | propositional without units |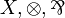 
|
| MLLu | propositional with units only |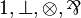 
|
| MLL0 | propositional with units and variables |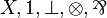 
|
| MLL1 | first-order without units |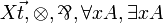 
|
| MLL01 | first-order with units |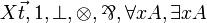 
|
| MLL2 | second-order propositional without units |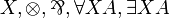 
|
| MLL02 | second-order propositional with units |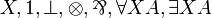 
|
| MLL12 | first-order and second-order without units |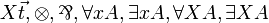 
|
| MLL012 | first-order and second-order with units |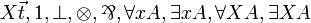 
|
[edit] Formulas and proof trees
[edit] Formulas
- First order quantification:
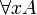with substitution A[t / x]
- Second order quantification:
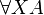with substitution A[B / X]
- Quantification of arbitrary order (mainly first or second):
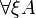with substitution A[τ / ξ]
[edit] Rule names
Name of the connective, followed by some additional information if required, followed by "L" for a left rule or "R" for a right rule. This is for a two-sided system, "R" is implicit for one-sided systems.
For example: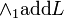 
.
[edit] Semantics
[edit] Coherent spaces
- Web of the space X:
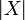
- Coherence relation of the space X: large
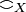and strict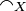 
[edit] Finiteness spaces
- Web of the finiteness space
: 
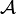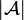
- Finiteness structure of the space :
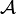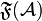(we use \mathfrak, which is consistent with the fact that 
).
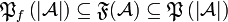[edit] Nets
- The free ports of a net R: fp(R).
- The result of the connection of two nets R and R', given the partial bijection
: 
.
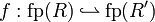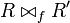- The number of loops in the resulting net:
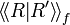(includes the loops already present in R and R').
[edit] Miscellaneous
- Isomorphism:
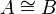
- injection:
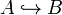
- partial injection:
