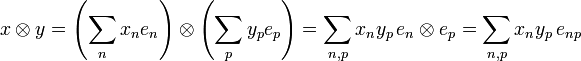GoI for MELL: exponentials
From LLWiki
(Difference between revisions)
(Creation of the page : generalities on Hilbert spaces tensor product) |
(→The tensor product of Hilbert spaces: presentation) |
||
| Line 1: | Line 1: | ||
| − | = The tensor product of Hilbert spaces</math> = |
+ | = The tensor product of Hilbert spaces = |
Recall that <math>(e_k)_{k\in\mathbb{N}}</math> is the canonical basis of <math>H=\ell^2(\mathbb{N})</math>. The space <math>H\tens H</math> is the collection of sequences <math>(x_{np})_{n,p\in\mathbb{N}}</math> of complex numbers such that: <math>\sum_{n,p}|x_{np}|^2</math> converges. The scalar product is defined just as before: |
Recall that <math>(e_k)_{k\in\mathbb{N}}</math> is the canonical basis of <math>H=\ell^2(\mathbb{N})</math>. The space <math>H\tens H</math> is the collection of sequences <math>(x_{np})_{n,p\in\mathbb{N}}</math> of complex numbers such that: <math>\sum_{n,p}|x_{np}|^2</math> converges. The scalar product is defined just as before: |
||
: <math>\langle (x_{np}), (y_{np})\rangle = \sum_{n,p} x_{np}\bar y_{np}</math>. |
: <math>\langle (x_{np}), (y_{np})\rangle = \sum_{n,p} x_{np}\bar y_{np}</math>. |
||
| − | |||
| − | The canonical basis of <math>H\tens H</math> is denoted <math>(e_{ij})_{i,j\in\mathbb{N}}</math> where <math>e_{ij}</math> is the (doubly indexed) sequence <math>(e_{ijnp})_{n,p\in\mathbb{N}}</math> defined by: |
||
| − | : <math>e_{ijnp} = \delta_{in}\delta_{jp}</math> (all terms are null but the one at index <math>(i,j)</math> which is 1). |
||
If <math>x = (x_n)_{n\in\mathbb{N}}</math> and <math>y = (y_p)_{p\in\mathbb{N}}</math> are vectors in <math>H</math> then their tensor is the sequence: |
If <math>x = (x_n)_{n\in\mathbb{N}}</math> and <math>y = (y_p)_{p\in\mathbb{N}}</math> are vectors in <math>H</math> then their tensor is the sequence: |
||
: <math>x\tens y = (x_ny_p)_{n,p\in\mathbb{N}}</math>. |
: <math>x\tens y = (x_ny_p)_{n,p\in\mathbb{N}}</math>. |
||
| − | In particular we have: <math>e_{ij} = e_i\tens e_j</math> and we can write: |
+ | In particular if we define: <math>e_{np} = e_n\tens e_p</math> so that <math>e_{np}</math> is the (doubly indexed) sequence of complex numbers given by <math>e_{npij} = \delta_{ni}\delta_{pj}</math> then <math>(e_{np})</math> is a hilbertian basis of <math>H\tens H</math>: the sequence <math>x=(x_{np})</math> may be written: |
| − | : <math>x\tens y = \left(\sum_n x_ne_n\right)\left(\sum_p y_pe_p\right) = |
+ | : <math>x = \sum_{n,p\in\mathbb{N}}x_{np}\,e_{np} |
| − | \sum_{n,p} x_ny_p e_n\tens e_p = \sum_{n,p} x_ny_p e_{np}</math> |
+ | = \sum_{n,p\in\mathbb{N}}x_{np}\,e_n\tens e_p</math>. |
| + | By bilinearity of tensor we have: |
||
| + | : <math>x\tens y = \left(\sum_n x_ne_n\right)\tens\left(\sum_p y_pe_p\right) = |
||
| + | \sum_{n,p} x_ny_p\, e_n\tens e_p = \sum_{n,p} x_ny_p\,e_{np}</math> |
||
Revision as of 11:20, 5 June 2010
The tensor product of Hilbert spaces
Recall that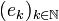 
is the canonical basis of 
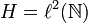. The space 
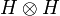is the collection of sequences 
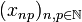of complex numbers such that:
| ∑ | | xnp | 2 |
| n,p |
converges. The scalar product is defined just as before:
-
.
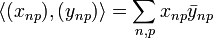If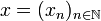 
and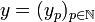 
are vectors in H then their tensor is the sequence:
-
.
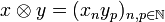In particular if we define: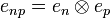 
so that enp is the (doubly indexed) sequence of complex numbers given by enpij = δniδpj then (enp) is a hilbertian basis of 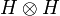: the sequence x = (xnp) may be written:
-
.
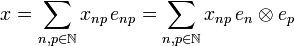By bilinearity of tensor we have:
