Translations of classical logic
From LLWiki
(Difference between revisions)
(T-translation) |
(Q-translation added) |
||
| Line 418: | Line 418: | ||
If we define <math>(\Gamma\vdash\Delta)^{\overline{T}} = \oc{\Gamma^{\overline{T}}}\vdash \Delta^{\overline{T}}</math>, we have <math>(\Gamma\vdash\Delta)^{\overline{T}} = (\Gamma\vdash\Delta)^T</math> and thus we obtain the same translation of proofs. |
If we define <math>(\Gamma\vdash\Delta)^{\overline{T}} = \oc{\Gamma^{\overline{T}}}\vdash \Delta^{\overline{T}}</math>, we have <math>(\Gamma\vdash\Delta)^{\overline{T}} = (\Gamma\vdash\Delta)^T</math> and thus we obtain the same translation of proofs. |
||
| + | |||
| + | |||
| + | == Q-translation <math>A\imp B \mapsto \oc{(A\limp\wn{B})}</math> == |
||
| + | |||
| + | Formulas are translated as: |
||
| + | |||
| + | <math> |
||
| + | \begin{array}{rcl} |
||
| + | X^Q & = & \oc{X} \\ |
||
| + | (A\imp B)^Q & = & \oc{(A^Q\limp\wn{B^Q})} \\ |
||
| + | (A\wedge B)^Q & = & \oc{(A^Q \tens B^Q)} \\ |
||
| + | T^Q & = & \oc{\one} \\ |
||
| + | (A\vee B)^Q & = & \oc{(A^Q\plus B^Q)} \\ |
||
| + | F^Q & = & \oc{\zero} \\ |
||
| + | (\neg A)^Q & = & \oc{(A^Q)\orth} \\ |
||
| + | (\forall\xi A)^Q & = & \oc{\forall\xi \wn{A^Q}} \\ |
||
| + | (\exists\xi A)^Q & = & \oc{\exists\xi A^Q} |
||
| + | \end{array} |
||
| + | </math> |
||
| + | |||
| + | The translation of any formula starts with <math>\oc</math>, we define <math>A^{\underline{Q}}</math> such that <math>A^Q=\oc{A^{\underline{Q}}}</math>. |
||
| + | |||
| + | The translation of sequents is <math>(\Gamma\vdash\Delta)^Q = \Gamma^Q\vdash\wn{\Delta^Q}</math>. |
||
| + | |||
| + | This allows one to translate the rules of classical logic into linear logic: |
||
| + | |||
| + | <math> |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{A\vdash A} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{A^Q\vdash A^Q} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{A^Q\vdash \wn{A^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,\Delta} |
||
| + | \AxRule{\Gamma',A\vdash \Delta'} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma,\Gamma'\vdash \Delta,\Delta'} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \AxRule{\Gamma'^Q,A^Q\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\Gamma'^Q,\wn{A^Q}\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma^Q,\Gamma'^Q\vdash \wn{\Delta^Q},\wn{\Delta'^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A,A\vdash \Delta} |
||
| + | \LabelRule{c L} |
||
| + | \UnaRule{\Gamma,A\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q,A^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc c L} |
||
| + | \UnaRule{\Gamma^Q,A^Q\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,A,\Delta} |
||
| + | \LabelRule{c R} |
||
| + | \UnaRule{\Gamma\vdash A,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{A^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\wn c R} |
||
| + | \UnaRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash \Delta} |
||
| + | \LabelRule{w L} |
||
| + | \UnaRule{\Gamma,A\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc w L} |
||
| + | \UnaRule{\Gamma^Q,A^Q\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash \Delta} |
||
| + | \LabelRule{w R} |
||
| + | \UnaRule{\Gamma\vdash A,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\wn w R} |
||
| + | \UnaRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A\vdash B,\Delta} |
||
| + | \LabelRule{\imp R} |
||
| + | \UnaRule{\Gamma\vdash A\imp B,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q\vdash \wn{B^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\limp R} |
||
| + | \UnaRule{\Gamma^Q\vdash A^Q\limp \wn{B^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{\Gamma^Q\vdash \oc{(A^Q\limp \wn{B^Q})},\wn{\Delta^Q}} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{\Gamma^Q\vdash \wn{\oc{(A^Q\limp \wn{B^Q})}},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,\Delta} |
||
| + | \AxRule{\Gamma',B\vdash \Delta'} |
||
| + | \LabelRule{\imp L} |
||
| + | \BinRule{\Gamma,\Gamma',A\imp B\vdash \Delta,\Delta'} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{A^Q\vdash A^Q} |
||
| + | \AxRule{\Gamma'^Q,B^Q\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\Gamma'^Q,\wn{B^Q}\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\limp L} |
||
| + | \BinRule{\Gamma'^Q,A^Q\limp \wn{B^Q},A^Q\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma'^Q,\oc{(A^Q\limp \wn{B^Q})},A^Q\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\Gamma'^Q,\oc{(A^Q\limp \wn{B^Q})},\wn{A^Q}\vdash \wn{\Delta'^Q}} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma^Q,\Gamma'^Q,\oc{(A^Q\limp \wn{B^Q})}\vdash \wn{\Delta^Q},\wn{\Delta'^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,\Delta} |
||
| + | \AxRule{\Gamma'\vdash B,\Delta'} |
||
| + | \LabelRule{\wedge R} |
||
| + | \BinRule{\Gamma,\Gamma'\vdash A\wedge B,\Delta,\Delta'} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \AxRule{\Gamma'^Q\vdash \wn{B^Q},\wn{\Delta'^Q}} |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{A^Q\vdash A^Q} |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{B^Q\vdash B^Q} |
||
| + | \LabelRule{\tens R} |
||
| + | \BinRule{A^Q,B^Q\vdash A^Q\tens B^Q} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{A^Q,B^Q\vdash \oc{(A^Q\tens B^Q)}} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{A^Q,B^Q\vdash \wn{\oc{(A^Q\tens B^Q)}}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{A^Q,\wn{B^Q}\vdash \wn{\oc{(A^Q\tens B^Q)}}} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma'^Q,A^Q\vdash \wn{\oc{(A^Q\tens B^Q)}},\wn{\Delta'^Q}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\Gamma'^Q,\wn{A^Q}\vdash \wn{\oc{(A^Q\tens B^Q)}},\wn{\Delta'^Q}} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma^Q,\Gamma'^Q\vdash \wn{\oc{(A^Q\tens B^Q)}},\wn{\Delta^Q},\wn{\Delta'^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A,B\vdash \Delta} |
||
| + | \LabelRule{\wedge L} |
||
| + | \UnaRule{\Gamma,A\wedge B\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q,B^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\tens L} |
||
| + | \UnaRule{\Gamma^Q,A^Q\tens B^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma^Q,\oc{(A^Q\tens B^Q)}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \LabelRule{T R} |
||
| + | \NulRule{{}\vdash T} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \LabelRule{\one R} |
||
| + | \NulRule{{}\vdash \one} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{{}\vdash \oc{\one}} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{{}\vdash \wn{\oc{\one}}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash \Delta} |
||
| + | \LabelRule{T L} |
||
| + | \UnaRule{\Gamma,T\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\one L} |
||
| + | \UnaRule{\Gamma^Q,\one\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma^Q,\oc{\one}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,\Delta} |
||
| + | \LabelRule{\vee_1 R} |
||
| + | \UnaRule{\Gamma\vdash A\vee B,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{A^Q\vdash A^Q} |
||
| + | \LabelRule{\plus_1 R} |
||
| + | \UnaRule{A^Q\vdash A^Q\plus B^Q} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{A^Q\vdash \oc{(A^Q\plus B^Q)}} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{A^Q\vdash \wn{\oc{(A^Q\plus B^Q)}}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\wn{A^Q}\vdash \wn{\oc{(A^Q\plus B^Q)}}} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma^Q\vdash \wn{\oc{(A^Q\plus B^Q)}},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A\vdash \Delta} |
||
| + | \AxRule{\Gamma,B\vdash \Delta} |
||
| + | \LabelRule{\vee L} |
||
| + | \BinRule{\Gamma,A\vee B\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q\vdash \wn{\Delta^Q}} |
||
| + | \AxRule{\Gamma^Q,B^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\plus L} |
||
| + | \BinRule{\Gamma^Q,A^Q\plus B^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma^Q,\oc{(A^Q\plus B^Q)}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \LabelRule{F L} |
||
| + | \NulRule{\Gamma,F\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \LabelRule{\zero L} |
||
| + | \NulRule{\Gamma^Q,\zero\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma^Q,\oc{\zero}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A\vdash \Delta} |
||
| + | \LabelRule{\neg R} |
||
| + | \UnaRule{\Gamma\vdash \neg A,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{(.)\orth R} |
||
| + | \UnaRule{\Gamma^Q\vdash (A^Q)\orth,\wn{\Delta^Q}} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{\Gamma^Q\vdash \oc{(A^Q)\orth},\wn{\Delta^Q}} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{\Gamma^Q\vdash \wn{\oc{(A^Q)\orth}},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,\Delta} |
||
| + | \LabelRule{\neg L} |
||
| + | \UnaRule{\Gamma,\neg A\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{(.)\orth L} |
||
| + | \UnaRule{\Gamma^Q,\oc{(A^Q)\orth}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A,\Delta} |
||
| + | \LabelRule{\forall R} |
||
| + | \UnaRule{\Gamma\vdash \forall\xi A,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\forall R} |
||
| + | \UnaRule{\Gamma^Q\vdash \forall\xi \wn{A^Q},\wn{\Delta^Q}} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{\Gamma^Q\vdash \oc{\forall\xi \wn{A^Q}},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | We use <math>(A[\tau/\xi])^Q=A^Q[\tau^{\underline{Q}}/\xi]</math>. |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A[\tau/\xi]\vdash \Delta} |
||
| + | \LabelRule{\forall L} |
||
| + | \UnaRule{\Gamma,\forall\xi A\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q[\tau^{\underline{Q}}/\xi]\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\Gamma^Q,\wn{A^Q[\tau^{\underline{Q}}/\xi]}\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\forall L} |
||
| + | \UnaRule{\Gamma^Q,\forall\xi \wn{A^Q}\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma^Q,\oc{\forall\xi \wn{A^Q}}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma\vdash A[\tau/\xi],\Delta} |
||
| + | \LabelRule{\exists R} |
||
| + | \UnaRule{\Gamma\vdash \exists\xi A,\Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q\vdash \wn{A^Q[\tau^{\underline{Q}}/\xi]},\wn{\Delta^Q}} |
||
| + | \LabelRule{\rulename{ax}} |
||
| + | \NulRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash A^Q[\tau^{\underline{Q}}/\xi]} |
||
| + | \LabelRule{\exists R} |
||
| + | \UnaRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash \exists\xi A^Q} |
||
| + | \LabelRule{\oc R} |
||
| + | \UnaRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash \oc{\exists\xi A^Q}} |
||
| + | \LabelRule{\wn d R} |
||
| + | \UnaRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash \wn{\oc{\exists\xi A^Q}}} |
||
| + | \LabelRule{\wn L} |
||
| + | \UnaRule{\wn{A^Q[\tau^{\underline{Q}}/\xi]}\vdash \wn{\oc{\exists\xi A^Q}}} |
||
| + | \LabelRule{\rulename{cut}} |
||
| + | \BinRule{\Gamma^Q\vdash \wn{\oc{\exists\xi A^Q}},\wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | <br /> |
||
| + | |||
| + | <math> |
||
| + | \AxRule{\Gamma,A\vdash \Delta} |
||
| + | \LabelRule{\exists L} |
||
| + | \UnaRule{\Gamma,\exists\xi A\vdash \Delta} |
||
| + | \DisplayProof |
||
| + | \qquad\mapsto\qquad |
||
| + | \AxRule{\Gamma^Q,A^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\exists L} |
||
| + | \UnaRule{\Gamma^Q,\exists\xi A^Q\vdash \wn{\Delta^Q}} |
||
| + | \LabelRule{\oc d L} |
||
| + | \UnaRule{\Gamma^Q,\oc{\exists\xi A^Q}\vdash \wn{\Delta^Q}} |
||
| + | \DisplayProof |
||
| + | </math> |
||
| + | |||
| + | |||
| + | === Alternative presentation === |
||
| + | |||
| + | It is also possible to define <math>A^{\underline{Q}}</math> as the primitive construction. |
||
| + | |||
| + | <math> |
||
| + | \begin{array}{rcl} |
||
| + | X^{\underline{Q}} & = & X \\ |
||
| + | (A\imp B)^{\underline{Q}} & = & \oc{A^{\underline{Q}}}\limp\wn{\oc{B^{\underline{Q}}}} \\ |
||
| + | (A\wedge B)^{\underline{Q}} & = & \oc{A^{\underline{Q}}}\tens\oc{B^{\underline{Q}}} \\ |
||
| + | T^{\underline{Q}} & = & \one \\ |
||
| + | (A\vee B)^{\underline{Q}} & = & \oc{A^{\underline{Q}}}\plus\oc{B^{\underline{Q}}} \\ |
||
| + | F^{\underline{Q}} & = & \zero \\ |
||
| + | (\neg A)^{\underline{Q}} & = & \wn{(A^{\underline{Q}})\orth} \\ |
||
| + | (\forall\xi A)^{\underline{Q}} & = & \forall\xi \wn{\oc{A^{\underline{Q}}}} \\ |
||
| + | (\exists\xi A)^{\underline{Q}} & = & \exists\xi \oc{A^{\underline{Q}}} |
||
| + | \end{array} |
||
| + | </math> |
||
| + | |||
| + | If we define <math>(\Gamma\vdash\Delta)^{\underline{Q}} = \oc{\Gamma^{\underline{Q}}}\vdash\wn{\oc{\Delta^{\underline{Q}}}}</math>, we have <math>(\Gamma\vdash\Delta)^{\underline{Q}} = (\Gamma\vdash\Delta)^Q</math> and thus we obtain the same translation of proofs. |
||
Latest revision as of 22:11, 5 October 2009
Contents |
[edit] T-translation 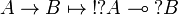
Formulas are translated as:
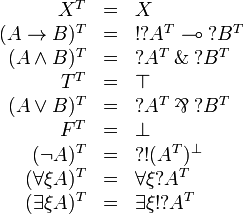
This is extended to sequents by 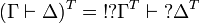 .
.
This allows one to translate the rules of classical logic into linear logic:
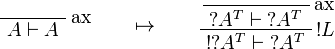
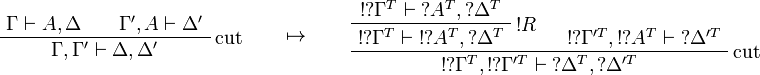
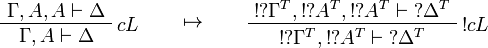
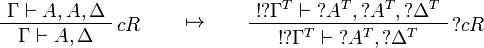
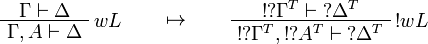
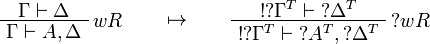
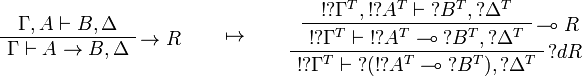
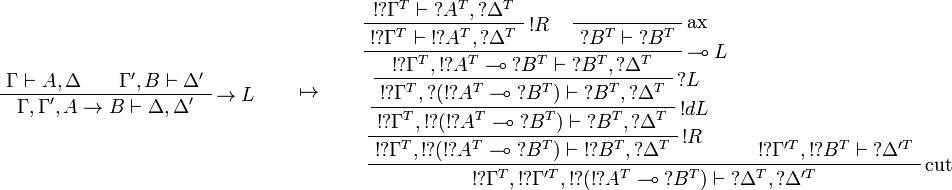
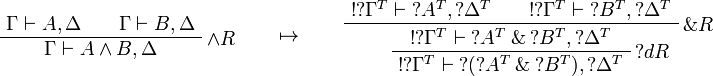
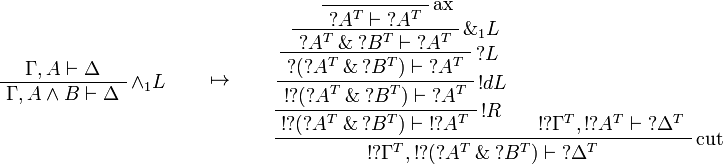
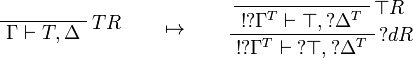
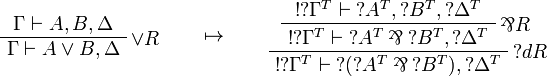
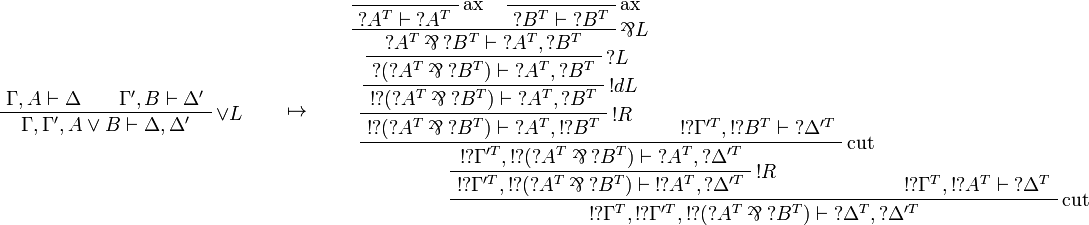
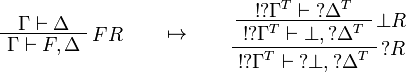
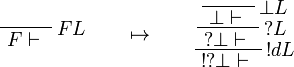
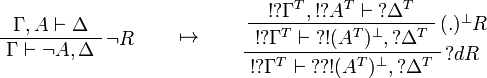
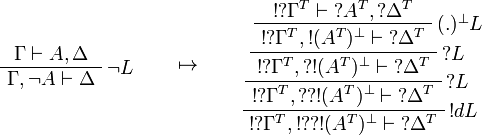
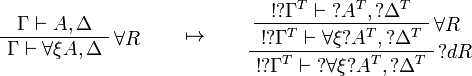
![\AxRule{\Gamma,A[\tau/\xi]\vdash \Delta}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\xi A\vdash \Delta}
\DisplayProof
\qquad\mapsto\qquad
\LabelRule{\rulename{ax}}
\NulRule{\wn{A^T}[\tau^T/\xi]\vdash \wn{A^T}[\tau^T/\xi]}
\LabelRule{\forall L}
\UnaRule{\forall\xi \wn{A^T}\vdash \wn{A^T}[\tau^T/\xi]}
\LabelRule{\wn L}
\UnaRule{\wn{\forall\xi \wn{A^T}}\vdash \wn{A^T}[\tau^T/\xi]}
\LabelRule{\oc d L}
\UnaRule{\oc{\wn{\forall\xi \wn{A^T}}}\vdash \wn{A^T}[\tau^T/\xi]}
\LabelRule{\oc R}
\UnaRule{\oc{\wn{\forall\xi \wn{A^T}}}\vdash \oc{\wn{A^T}}[\tau^T/\xi]}
\AxRule{\oc{\wn{\Gamma^T}},\oc{\wn{(A^T[\tau^T/\xi])}}\vdash \wn{\Delta^T}}
\LabelRule{\rulename{cut}}
\BinRule{\oc{\wn{\Gamma^T}},\oc{\wn{\forall\xi \wn{A^T}}}\vdash \wn{\Delta^T}}
\DisplayProof](/mediawiki/images/math/3/4/1/341f09878b944f3cb72078aea55a1218.png)
![\AxRule{\Gamma\vdash A[\tau/\xi],\Delta}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash \exists\xi A,\Delta}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\oc{\wn{\Gamma^T}}\vdash \wn{A^T[\tau^T/\xi]},\wn{\Delta^T}}
\LabelRule{\oc R}
\UnaRule{\oc{\wn{\Gamma^T}}\vdash \oc{\wn{A^T[\tau^T/\xi]}},\wn{\Delta^T}}
\LabelRule{\exists R}
\UnaRule{\oc{\wn{\Gamma^T}}\vdash \exists\xi \oc{\wn{A^T}},\wn{\Delta^T}}
\LabelRule{\wn d R}
\UnaRule{\oc{\wn{\Gamma^T}}\vdash \wn{\exists\xi \oc{\wn{A^T}}},\wn{\Delta^T}}
\DisplayProof](/mediawiki/images/math/3/2/d/32d1eee4c86605757d3c638a40b79cc6.png)
[edit] Alternative presentation
It is also possible to define 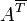 by:
by:
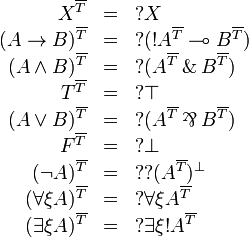
If we define 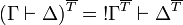 , we have
, we have 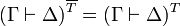 and thus we obtain the same translation of proofs.
and thus we obtain the same translation of proofs.
[edit] Q-translation 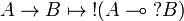
Formulas are translated as:
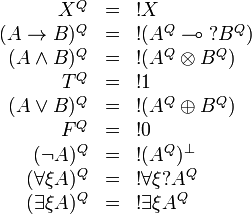
The translation of any formula starts with 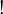 , we define
, we define 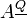 such that
such that 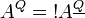 .
.
The translation of sequents is 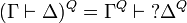 .
.
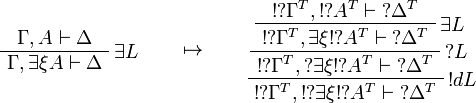
This allows one to translate the rules of classical logic into linear logic:
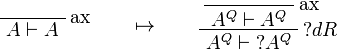
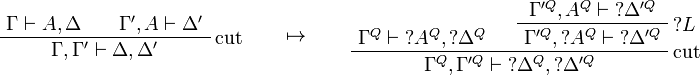
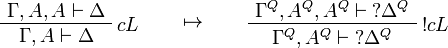
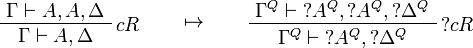
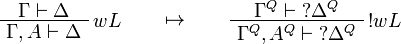

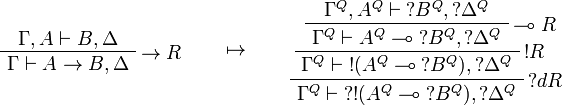
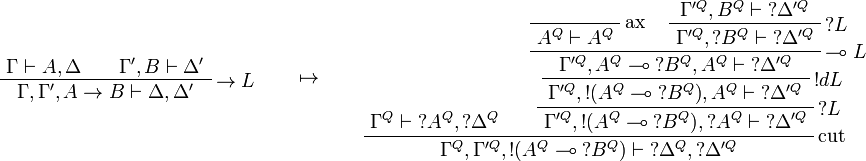
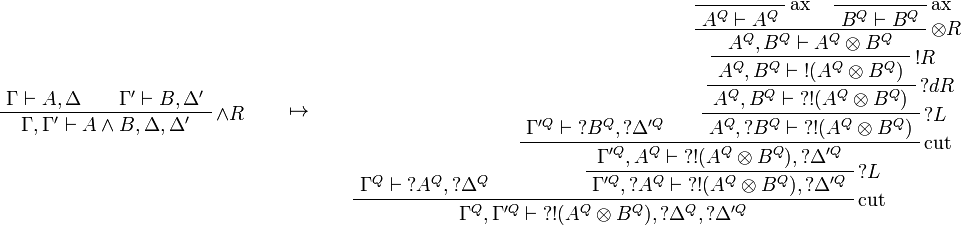
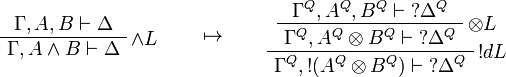
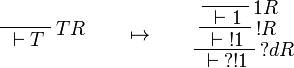
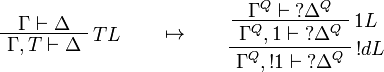
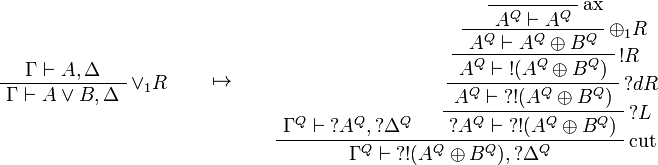
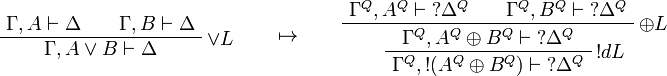
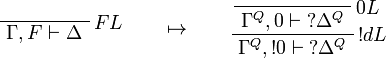
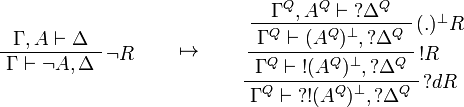
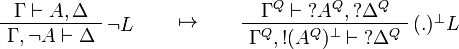
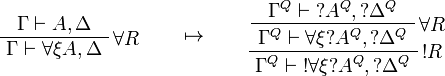
We use ![(A[\tau/\xi])^Q=A^Q[\tau^{\underline{Q}}/\xi]](/mediawiki/images/math/0/a/e/0aef96b95b5a70a52b6ef6f992756077.png) .
.
![\AxRule{\Gamma,A[\tau/\xi]\vdash \Delta}
\LabelRule{\forall L}
\UnaRule{\Gamma,\forall\xi A\vdash \Delta}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\Gamma^Q,A^Q[\tau^{\underline{Q}}/\xi]\vdash \wn{\Delta^Q}}
\LabelRule{\wn L}
\UnaRule{\Gamma^Q,\wn{A^Q[\tau^{\underline{Q}}/\xi]}\vdash \wn{\Delta^Q}}
\LabelRule{\forall L}
\UnaRule{\Gamma^Q,\forall\xi \wn{A^Q}\vdash \wn{\Delta^Q}}
\LabelRule{\oc d L}
\UnaRule{\Gamma^Q,\oc{\forall\xi \wn{A^Q}}\vdash \wn{\Delta^Q}}
\DisplayProof](/mediawiki/images/math/f/8/a/f8ab5b743d2740a9054a7c2926e22bd8.png)
![\AxRule{\Gamma\vdash A[\tau/\xi],\Delta}
\LabelRule{\exists R}
\UnaRule{\Gamma\vdash \exists\xi A,\Delta}
\DisplayProof
\qquad\mapsto\qquad
\AxRule{\Gamma^Q\vdash \wn{A^Q[\tau^{\underline{Q}}/\xi]},\wn{\Delta^Q}}
\LabelRule{\rulename{ax}}
\NulRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash A^Q[\tau^{\underline{Q}}/\xi]}
\LabelRule{\exists R}
\UnaRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash \exists\xi A^Q}
\LabelRule{\oc R}
\UnaRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash \oc{\exists\xi A^Q}}
\LabelRule{\wn d R}
\UnaRule{A^Q[\tau^{\underline{Q}}/\xi]\vdash \wn{\oc{\exists\xi A^Q}}}
\LabelRule{\wn L}
\UnaRule{\wn{A^Q[\tau^{\underline{Q}}/\xi]}\vdash \wn{\oc{\exists\xi A^Q}}}
\LabelRule{\rulename{cut}}
\BinRule{\Gamma^Q\vdash \wn{\oc{\exists\xi A^Q}},\wn{\Delta^Q}}
\DisplayProof](/mediawiki/images/math/9/c/f/9cf2a4f59e25676577e9a3566035eb8e.png)
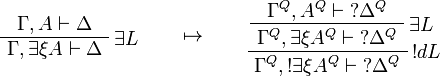
[edit] Alternative presentation
It is also possible to define 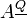 as the primitive construction.
as the primitive construction.
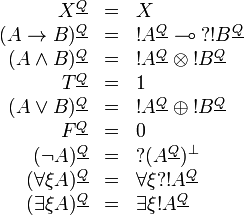
If we define 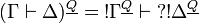 , we have
, we have 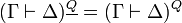 and thus we obtain the same translation of proofs.
and thus we obtain the same translation of proofs.