Finiteness semantics
Lionel Vaux (Talk | contribs) m (fixed display math) |
Lionel Vaux (Talk | contribs) m (→Finiteness spaces: link to closure operators) |
||
| Line 7: | Line 7: | ||
== Finiteness spaces == |
== Finiteness spaces == |
||
| − | The construction of finiteness spaces follows a well known pattern. It is given by the following notion of orthogonality: <math>a\mathrel \bot a'</math> iff <math>a\cap a'</math> is finite. Then one unrolls familiar definitions, as we do in the following paragraphs. |
+ | The construction of finiteness spaces follows a well known pattern. It is given by the following notion of orthogonality: <math>a\mathrel \bot a'</math> iff <math>a\cap a'</math> is finite. Then one unrolls [[Phase_semantics#Closure_operators|familiar definitions]], as we do in the following paragraphs. |
Let <math>A</math> be a set. Denote by <math>\mathfrak P(A)</math> the powerset of <math>A</math> and by <math>\mathfrak P_f(A)</math> the set of all finite subsets of <math>A</math>. Let <math>{\mathfrak F} \subseteq \mathfrak P(A)</math> any set of subsets of <math>A</math>. We define the pre-dual of <math>{\mathfrak F}</math> in <math>A</math> as <math>{\mathfrak F}^{\bot_{A}}=\left\{a'\subseteq A;\ \forall a\in{\mathfrak F},\ a\cap a'\in\mathfrak P_f(A)\right\}</math>. In general we will omit the subscript in the pre-dual notation and just write <math>{\mathfrak F}\orth</math>. For all <math>{\mathfrak F}\subseteq\mathfrak P(A)</math>, we have the following immediate properties: <math>\mathfrak P_f(A) \subseteq {\mathfrak F}\orth</math>; <math>{\mathfrak F}\subseteq {\mathfrak F}\biorth</math>; if <math>{\mathfrak G}\subseteq{\mathfrak F}</math>, <math>{\mathfrak F}\orth\subseteq {\mathfrak G}\orth</math>. By the last two, we get <math>{\mathfrak F}\orth = {\mathfrak F}\triorth</math>. A finiteness structure on <math>A</math> is then a set <math>{\mathfrak F}</math> of subsets of <math>A</math> such that <math>{\mathfrak F}\biorth = {\mathfrak F}</math>. |
Let <math>A</math> be a set. Denote by <math>\mathfrak P(A)</math> the powerset of <math>A</math> and by <math>\mathfrak P_f(A)</math> the set of all finite subsets of <math>A</math>. Let <math>{\mathfrak F} \subseteq \mathfrak P(A)</math> any set of subsets of <math>A</math>. We define the pre-dual of <math>{\mathfrak F}</math> in <math>A</math> as <math>{\mathfrak F}^{\bot_{A}}=\left\{a'\subseteq A;\ \forall a\in{\mathfrak F},\ a\cap a'\in\mathfrak P_f(A)\right\}</math>. In general we will omit the subscript in the pre-dual notation and just write <math>{\mathfrak F}\orth</math>. For all <math>{\mathfrak F}\subseteq\mathfrak P(A)</math>, we have the following immediate properties: <math>\mathfrak P_f(A) \subseteq {\mathfrak F}\orth</math>; <math>{\mathfrak F}\subseteq {\mathfrak F}\biorth</math>; if <math>{\mathfrak G}\subseteq{\mathfrak F}</math>, <math>{\mathfrak F}\orth\subseteq {\mathfrak G}\orth</math>. By the last two, we get <math>{\mathfrak F}\orth = {\mathfrak F}\triorth</math>. A finiteness structure on <math>A</math> is then a set <math>{\mathfrak F}</math> of subsets of <math>A</math> such that <math>{\mathfrak F}\biorth = {\mathfrak F}</math>. |
||
Revision as of 19:30, 22 May 2009
The category 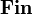 of finiteness spaces and finitary relations was introduced by Ehrhard, refining the purely relational model of linear logic. A finiteness space is a set equipped with a finiteness structure, i.e. a particular set of subsets which are said to be finitary; and the model is such that the usual relational denotation of a proof in linear logic is always a finitary subset of its conclusion. By the usual co-Kleisli construction, this also provides a model of the simply typed lambda-calculus: the cartesian closed category
of finiteness spaces and finitary relations was introduced by Ehrhard, refining the purely relational model of linear logic. A finiteness space is a set equipped with a finiteness structure, i.e. a particular set of subsets which are said to be finitary; and the model is such that the usual relational denotation of a proof in linear logic is always a finitary subset of its conclusion. By the usual co-Kleisli construction, this also provides a model of the simply typed lambda-calculus: the cartesian closed category 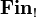 .
.
The main property of finiteness spaces is that the intersection of two finitary subsets of dual types is always finite. This feature allows to reformulate Girard's quantitative semantics in a standard algebraic setting, where morphisms interpreting typed λ-terms are analytic functions between the topological vector spaces generated by vectors with finitary supports. This provided the semantical foundations of Ehrhard-Regnier's differential λ-calculus and motivated the general study of a differential extension of linear logic.
It is worth noticing that finiteness spaces can accomodate typed λ-calculi only: for instance, the relational semantics of fixpoint combinators is never finitary. The whole point of the finiteness construction is actually to reject infinite computations. Indeed, from a logical point of view, computation is cut elimination: the finiteness structure ensures the intermediate sets involved in the relational interpretation of a cut are all finite. In that sense, the finitary semantics is intrinsically typed.
Contents |
Finiteness spaces
The construction of finiteness spaces follows a well known pattern. It is given by the following notion of orthogonality: 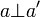 iff
iff 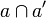 is finite. Then one unrolls familiar definitions, as we do in the following paragraphs.
is finite. Then one unrolls familiar definitions, as we do in the following paragraphs.
Let A be a set. Denote by 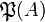 the powerset of A and by
the powerset of A and by 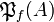 the set of all finite subsets of A. Let
the set of all finite subsets of A. Let 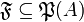 any set of subsets of A. We define the pre-dual of
any set of subsets of A. We define the pre-dual of 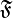 in A as
in A as 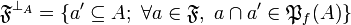 . In general we will omit the subscript in the pre-dual notation and just write
. In general we will omit the subscript in the pre-dual notation and just write 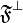 . For all
. For all 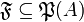 , we have the following immediate properties:
, we have the following immediate properties: 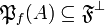 ;
; 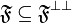 ; if
; if 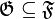 ,
, 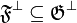 . By the last two, we get
. By the last two, we get 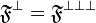 . A finiteness structure on A is then a set
. A finiteness structure on A is then a set 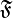 of subsets of A such that
of subsets of A such that 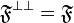 .
.
A finiteness space is a dependant pair 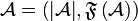 where
where 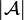 is the underlying set (the web of
is the underlying set (the web of 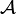 ) and
) and 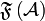 is a finiteness structure on
is a finiteness structure on 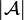 . We then write
. We then write 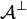 for the dual finiteness space:
for the dual finiteness space: 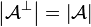 and
and 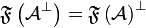 . The elements of
. The elements of 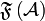 are called the finitary subsets of
are called the finitary subsets of 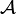 .
.
Example.
For all set A, 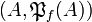 is a finiteness space and
is a finiteness space and 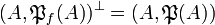 . In particular, each finite set A is the web of exactly one finiteness space:
. In particular, each finite set A is the web of exactly one finiteness space: 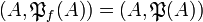 . We introduce the following two:
. We introduce the following two: 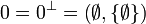 and
and 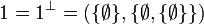 . We also introduce the finiteness space of natural numbers
. We also introduce the finiteness space of natural numbers 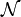 by:
by: 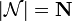 and
and 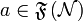 iff a is finite. We write
iff a is finite. We write 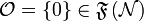 .
.
Notice that 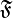 is a finiteness structure iff it is of the form
is a finiteness structure iff it is of the form 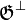 . It follows that any finiteness structure
. It follows that any finiteness structure 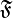 is downwards closed for inclusion, and closed under finite unions and arbitrary intersections. Notice however that
is downwards closed for inclusion, and closed under finite unions and arbitrary intersections. Notice however that 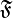 is not closed under directed unions in general: for all
is not closed under directed unions in general: for all 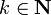 , write
, write 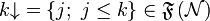 ; then
; then 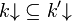 as soon as
as soon as 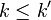 , but
, but 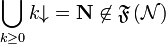 .
.
Multiplicatives
For all finiteness spaces 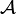 and
and 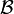 , we define
, we define 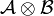 by
by 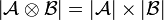 and
and 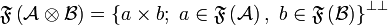 . It can be shown that
. It can be shown that 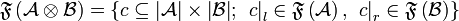 , where
, where 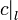 and
and 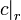 are the obvious projections.
are the obvious projections.
Let 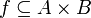 be a relation from A to B, we write
be a relation from A to B, we write 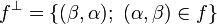 . For all
. For all 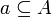 , we set
, we set 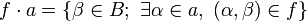 . If moreover
. If moreover 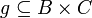 , we define
, we define 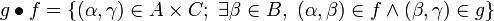 . Then, setting
. Then, setting 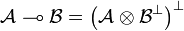 ,
, 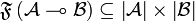 is characterized as follows:
\begin{center}
\begin{tabular}{r@{\ iff\ }l}
is characterized as follows:
\begin{center}
\begin{tabular}{r@{\ iff\ }l}
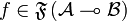 &
& 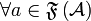 ,
, 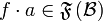 and
and 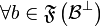 ,
, 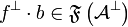 \\
&
\\
& 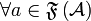 ,
, 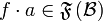 and
and 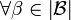 ,
, 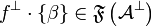 \\
&
\\
& 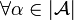 ,
, 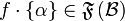 and
and 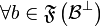 ,
, 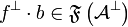 \end{tabular}
\end{center}
The elements of
\end{tabular}
\end{center}
The elements of 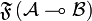 are called finitary relations from
are called finitary relations from 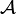 to
to 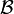 . By the previous characterization, the identity relation
. By the previous characterization, the identity relation 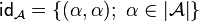 is finitary, and the composition of two finitary relations is also finitary. One can thus define the category
is finitary, and the composition of two finitary relations is also finitary. One can thus define the category 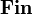 of finiteness spaces and finitary relations: the objects of
of finiteness spaces and finitary relations: the objects of 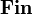 are all finiteness spaces, and
are all finiteness spaces, and 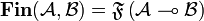 . Equipped with the tensor product
. Equipped with the tensor product 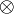 ,
,  is symmetric monoidal, with unit
is symmetric monoidal, with unit 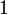 ; it is monoidal closed by the definition of
; it is monoidal closed by the definition of 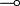 ; it is * -autonomous by the obvious isomorphism between
; it is * -autonomous by the obvious isomorphism between 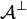 and
and 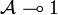 .
.
Example.
Setting 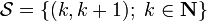 and
and 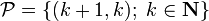 , we have
, we have 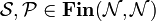 and
and 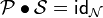 .
.
Additives
We now introduce the cartesian structure of  . We define
. We define 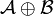 by
by 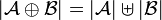 and
and 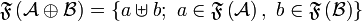 where
where 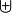 denotes the disjoint union of sets:
denotes the disjoint union of sets: 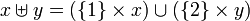 . We have
. We have 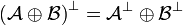 . The category
. The category 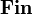 is both cartesian and co-cartesian, with
is both cartesian and co-cartesian, with  being the product and co-product, and
being the product and co-product, and 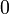 the initial and terminal object. Projections are given by:
\begin{eqnarray*}
\lambda_{{\mathcal A},{\mathcal B}}&=&\left\{\left((1,\alpha),\alpha\right);\ \alpha\in\web{\mathcal A}\right\}
\in\mathbf{Fin}({\mathcal A}\oplus{\mathcal B},{\mathcal A}) \\
\rho_{{\mathcal A},{\mathcal B}}&=&\left\{\left((2,\beta),\beta\right);\ \beta\in\web{\mathcal B}\right\}
\in\mathbf{Fin}({\mathcal A}\oplus{\mathcal B},{\mathcal B})
\end{eqnarray*}
and if
the initial and terminal object. Projections are given by:
\begin{eqnarray*}
\lambda_{{\mathcal A},{\mathcal B}}&=&\left\{\left((1,\alpha),\alpha\right);\ \alpha\in\web{\mathcal A}\right\}
\in\mathbf{Fin}({\mathcal A}\oplus{\mathcal B},{\mathcal A}) \\
\rho_{{\mathcal A},{\mathcal B}}&=&\left\{\left((2,\beta),\beta\right);\ \beta\in\web{\mathcal B}\right\}
\in\mathbf{Fin}({\mathcal A}\oplus{\mathcal B},{\mathcal B})
\end{eqnarray*}
and if 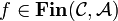 and
and 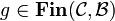 , pairing is given by:
, pairing is given by:
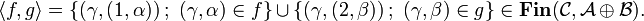
The unique morphism from 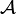 to
to 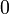 is the empty relation. The co-cartesian structure is obtained symmetrically.
is the empty relation. The co-cartesian structure is obtained symmetrically.
Example.
Write 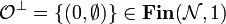 . Then
. Then 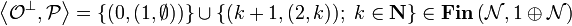 is an isomorphism.
is an isomorphism.
Exponentials
If A is a set, we denote by 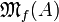 the set of all finite multisets of
elements of A, and if
the set of all finite multisets of
elements of A, and if 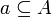 , we write
, we write 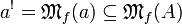 .
If
.
If 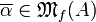 , we denote its support by
, we denote its support by
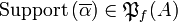 . For all finiteness space
. For all finiteness space 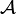 , we define
, we define
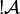 by:
by: 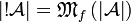 and
and 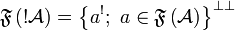 .
It can be shown that
.
It can be shown that 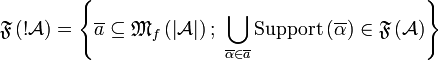 .
Then, for all
.
Then, for all 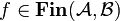 , we set
, we set
![\oc f =\left\{\left(\left[\alpha_1,\ldots,\alpha_n\right],\left[\beta_1,\ldots,\beta_n\right]\right);\ \forall i,\ (\alpha_i,\beta_i)\in f\right\} \in \mathbf{Fin}(\oc {\mathcal A}, \oc {\mathcal B}),](/mediawiki/images/math/b/2/f/b2f34984c0cb2d7403a8ae3d3e7febe3.png)
which defines a functor.
Natural transformations
![\mathsf{der}_{{\mathcal A}}=\left\{([\alpha],\alpha);\ \alpha\in \web{{\mathcal A}}\right\}\in\mathbf{Fin}(\oc{\mathcal A},{\mathcal A})](/mediawiki/images/math/3/4/a/34a5940f73335627eb8d19f1f3e3371e.png) and
and
![\mathsf{digg}_{{\mathcal A}}=\left\{\left(\sum_{i=1}^n\overline\alpha_i,\left[\overline\alpha_1,\ldots,\overline\alpha_n\right]\right);\ \forall i,\ \overline\alpha_i\in\web{\oc {\mathcal A}}\right\}](/mediawiki/images/math/a/8/0/a80ae2d100f55cc252774621422d0bcc.png) make this functor a comonad.
make this functor a comonad.
Example.
We have isomorphisms
![\left\{([],\emptyset)\right\}\in\mathbf{Fin}(\oc\zero,\one)](/mediawiki/images/math/1/9/e/19eeee98d64e829cd46b47bc879a348e.png) and
and
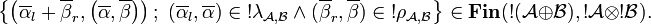
More generally, we have
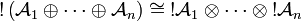 .
.