Talk:Sequent calculus
From LLWiki
(Difference between revisions)
(→Quantifiers) |
(→Quantifiers: closed topic) |
||
| Line 1: | Line 1: | ||
| − | == Quantifiers == |
||
| − | |||
| − | The presentation does not seem to be completely uniform concerning quantifiers: are first-order quantifiers taken into account? It would be nice. |
||
| − | |||
| − | A few related points: |
||
| − | * Why a distinction between atomic formulas and propositional variables? |
||
| − | * Some mixing between <math>\forall x A</math> and <math>\forall X A</math>. I tried to propose a [[notations#formulas|convention]] on that point, but it does not match here with the use of <math>\alpha</math> for atoms. |
||
| − | * Define immediate subformula of <math>\forall X A</math> as <math>A</math>? |
||
| − | -- [[User:Olivier Laurent|Olivier Laurent]] 18:37, 14 January 2009 (UTC) |
||
| − | |||
| − | :I improved the uniformity for quantifiers: the full system with first and second order quantification is described, only predicate variables with first-order arguments are not described. |
||
| − | :The distinction between atomic formulas and propositional variables is because there are systems with atomic formulas that are not propositional variables but fixed predicates like equalities. |
||
| − | :I found <math>\alpha</math> to be a used notation for atomic formulas in other texts, so I used <math>\xi,\psi,\zeta</math> instead for arbitrary variables. |
||
| − | |||
| − | :Using substitution in the definition of subformulas is questionable, but if the only immediate subformula of <math>\forall\xi.A</math> is <math>A</math>, then the ''subformula'' property does not hold. |
||
| − | |||
| − | :''Edit:'' Well... my bad. The subformula property does hold if the only immediate subformula of <math>\forall\xi.A</math> is <math>A</math>, substitution is necessary only for <math>\exists\xi.A</math>. I changed it. |
||
| − | |||
| − | :-- [[User:Emmanuel Beffara|Emmanuel Beffara]] |
||
| − | |||
== Two-sided sequent calculus == |
== Two-sided sequent calculus == |
||
Revision as of 16:45, 14 March 2009
Two-sided sequent calculus
I think the terminology "two-sided sequent calculus" should be used for the system where all the connectives are involved and all the rules are duplicated (with respect to the one-sided version) and negation is a connective.
In this way, we obtain the one-sided version from the two-sided one by:
- quotient the formulas by de Morgan laws and get negation only on atoms, negation is defined for compound formulas (not a connective)
- fold all the rules by
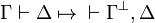
- remove useless rules (negation rules become identities, almost all the rules appear twice)
A possible name for the two-sided system presented here could be "two-sided positive sequent calculus".
-- Olivier Laurent 21:34, 15 January 2009 (UTC)