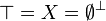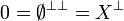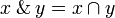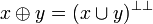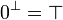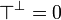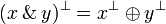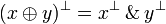Revision as of 15:16, 8 February 2009

Introduction

The semantics given by phase spaces is a kind of "formula and provability semantics", and is thus quite different in spirit from the more usual denotational semantics of linear logic. (Those are rather some "formulas and proofs semantics".)

 --- probably a whole lot more of blabla to put here... ---

Preliminaries: relation and closure operators

Part of the structure obtained from phase semantics works in a very general framework and relies solely on the notion of relation between two sets.

Relations and operators on subsets

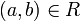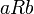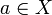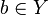The starting point of phase semantics is the notion of duality. The structure needed to talk about duality is very simple: one just needs a relation $R$ between two sets $X$ and $Y$ . Using standard mathematical practice, we can write either $(a,b) \in R$ or $a\mathrel{R} b$ to say that $a\in X$ and $b\in Y$ are related.

Definition

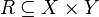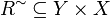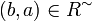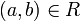If $R\subseteq X\times Y$ is a relation, we write $R^\sim\subseteq Y\times X$ for the converse relation: $(b,a)\in R^\sim$ iff $(a,b)\in R$ .

Such a relation yields three interesting operators sending subsets of $X$ to subsets of $Y$ :

Definition

Let 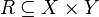$R\subseteq X\times Y$ be a relation, define the operators 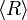$\langle R\rangle$ , $[R]$ and $_R$ taking subsets of $X$ to subsets of $Y$ as follows:

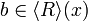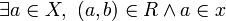
$b\in\langle R\rangle(x)$ iff $\exists a\in X,\ (a,b)\in R \land a\in x$
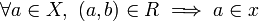
$b\in[R](x)$ iff $\forall a\in X,\ (a,b)\in R \implies a\in x$
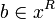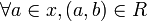
$b\in x^R$ iff $\forall a\in x, (a,b)\in R$

The operator 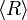$\langle R\rangle$ is usually called the direct image of the relation, $[R]$ is sometimes called the universal image of the relation.

It is trivial to check that 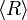$\langle R\rangle$ and $[R]$ are covariant (increasing for the 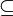$\subseteq$ relation) while $_R$ is contravariant (decreasing for the 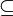$\subseteq$ relation). More interesting:

Lemma (Galois Connections)

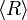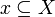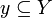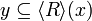
$\langle R\rangle$ is right-adjoint to $[R ˜]$ : for any $x\subseteq X$ and $y\subseteq Y$ , we have $[R^\sim]y \subseteq x$ iff $y\subseteq \langle R\rangle(x)$
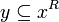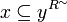
we have $y\subseteq x^R$ iff $x\subseteq y^{R^\sim}$

This implies directly that 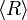$\langle R\rangle$ commutes with arbitrary unions and $[R]$ commutes with arbitrary intersections. (And in fact, any operator commuting with arbitrary unions (resp. intersections) is of the form 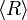$\langle R\rangle$ (resp. $[R]$ ).

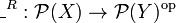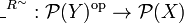Remark: the operator $_R$ sends unions to intersections because $\_^R : \mathcal{P}(X) \to \mathcal{P}(Y)^\mathrm{op}$ is right adjoint to $\_^{R^\sim} : \mathcal{P}(Y)^{\mathrm{op}} \to \mathcal{P}(X)$ ...

Closure operators

Definition

A closure operator on 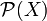$\mathcal{P}(X)$ is an monotonic increasing operator $P$ on the subsets of $X$ which satisfies:

for all 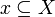$x\subseteq X$ , we have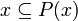 $x\subseteq P(x)$
for all 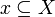$x\subseteq X$ , we have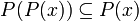 $P(P(x))\subseteq P(x)$

Closure operators are quite common in mathematics and computer science. They correspond exactly to the notion of monad on a preorder...

Lemma

Write 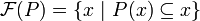$\mathcal{F}(P) = \{x\ |\ P(x)\subseteq x\}$ for the collection of fixed points of a closure operator $P$ . We have that 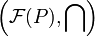$\left(\mathcal{F}(P),\bigcap\right)$ is a complete inf-lattice.

Since any complete inf-lattice is automatically a complete sup-lattice, 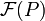$\mathcal{F}(P)$ is also a complete sup-lattice. However, the sup operation isn't given by plain union:

Lemma

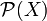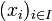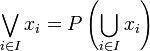If $P$ is a closure operator on $\mathcal{P}(X)$ , and if $(x_i)_{i\in I}$ is a (possibly infinite) family of subsets of $X$ , we write $\bigvee_{i\in I} x_i = P\left(\bigcup_{i\in I} x_i\right)$ .

We have 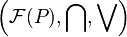$\left(\mathcal{F}(P),\bigcap,\bigvee\right)$ is a complete lattice.

Proof. easy.

A rather direct consequence of the Galois connections of the previous section is:

Lemma

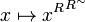The operator and $\langle R\rangle \circ [R^\sim]$ and the operator $x\mapsto {x^R}^{R^\sim}$ are closures.

A last trivial lemma:

Lemma

We have 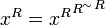$x^R = {{x^R}^{R^\sim}}^{R}$ .

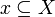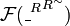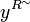As a consequence, a subset $x\subseteq X$ is in $\mathcal{F}({\_^R}^{R^\sim})$ iff it is of the form $y^{R^\sim}$ .

Remark: everything gets a little simpler when $R$ is a symmetric relation on $X$ .

Phase Semantics

Phase spaces

Definition (monoid)

A monoid is simply a set $X$ equipped with a binary operation $\_\cdot\_$ s.t.:

the operation is associative
there is a neutral element $1\in X$

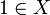
The monoid is commutative when the binary operation is commutative.

Definition (Phase space)

A phase space is given by:

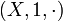a commutative monoid $(X,1,\cdot)$ ,
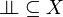together with a subset $\bot\!\!\!\bot\subseteq X$ .

The elements of $X$ are called phases.

We write 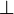$\bot$ for the relation 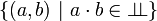$\{(a,b)\ |\ a\cdot b \in \bot\!\!\!\bot\}$ . This relation is symmetric.

A fact in a phase space is simply a fixed point for the closure operator 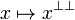$x\mapsto x\biorth$ .

Thanks to the preliminary work, we have:

Corollary

The set of facts of a phase space is a complete lattice where:

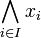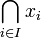$\bigwedge_{i\in I} x_i$ is simply $\bigcap_{i\in I} x_i$ ,
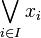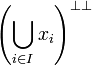$\bigvee_{i\in I} x_i$ is $\left(\bigcup_{i\in I} x_i\right)\biorth$ .

Additive connectives

The previous corollary makes the following definition correct:

Definition (additive connectives)

If 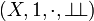$(X,1,\cdot,\bot\!\!\bot)$ is a phase space, we define the following facts and operations on facts:

$\top = X = \emptyset\orth$
$\zero = \emptyset\biorth = X\orth$
$x\with y = x\cap y$
$x\plus y = (x\cup y)\biorth$

Once again, the next lemma follows from previous observations:

Lemma (additive de Morgan laws)

We have

$\zero\orth = \top$
$\top\orth = \zero$
$(x\with y)\orth = x\orth \plus y\orth$
$(x\plus y)\orth = x\orth \with y\orth$

Multiplicative connectives

In order to define the multiplicative connectives, we actually need to use the monoid structure of our phase space.

--- TODO: I'll try to do it soon, but volonteers are welcome --- Pierre Hyvernat 11:50, 8 February 2009 (UTC) ---

@@ Line 104: / Line 104: @@
 We write <math>\bot</math> for the relation <math>\{(a,b)\ |\ a\cdot b \in \bot\!\!\!\bot\}</math>. This relation is symmetric.
-A ''fact'' in a phase space is simply a fixed point for the closure operator <math>x\mapsto x^{\bot\bot}</math>.
+A ''fact'' in a phase space is simply a fixed point for the closure operator <math>x\mapsto x\biorth</math>.
 }}
@@ Line 113: / Line 113: @@
 The set of facts of a phase space is a complete lattice where:
 # <math>\bigwedge_{i\in I} x_i</math> is simply <math>\bigcap_{i\in I} x_i</math>,
-# <math>\bigvee_{i\in I} x_i</math> is <math>\left(\bigcup_{i\in I} x_i\right)^{\bot\bot}</math>.
+# <math>\bigvee_{i\in I} x_i</math> is <math>\left(\bigcup_{i\in I} x_i\right)\biorth</math>.
 }}
@@ Line 122: / Line 122: @@
 {{Definition|title=additive connectives|
 If <math>(X,1,\cdot,\bot\!\!\bot)</math> is a phase space, we define the following facts and operations on facts:
-# <math>\top = X = \emptyset^\bot</math>
+# <math>\top = X = \emptyset\orth</math>
-# <math>\zero = \emptyset^{\bot\bot} = X^\bot</math>
+# <math>\zero = \emptyset\biorth = X\orth</math>
 # <math>x\with y = x\cap y</math>
-# <math>x\plus y = (x\cup y)^{\bot\bot}</math>
+# <math>x\plus y = (x\cup y)\biorth</math>
 }}
@@ Line 132: / Line 132: @@
 {{Lemma|title=additive de Morgan laws|
 We have
-# <math>\zero^\bot = \top</math>
+# <math>\zero\orth = \top</math>
-# <math>\top^\bot = \zero</math>
+# <math>\top\orth = \zero</math>
-# <math>(x\with y)^\bot = x^\bot \plus y^\bot</math>
+# <math>(x\with y)\orth = x\orth \plus y\orth</math>
-# <math>(x\plus y)^\bot = x^\bot \with y^\bot</math>
+# <math>(x\plus y)\orth = x\orth \with y\orth</math>
 }}

Phase semantics

Revision as of 15:16, 8 February 2009

Contents

Introduction

Preliminaries: relation and closure operators

Relations and operators on subsets

Closure operators

Phase Semantics

Phase spaces

Additive connectives

Multiplicative connectives

Exponentials

Completeness

The Rest

Views

Personal tools

Navigation

Search

Tools